Нелінійні множинні економетричні моделі та їх аналіз.
Нехай економетрична модель у матричній формі має вигляд Y = ХА + и, (1) де Y – вектор значень залежної змінної; X – матриця незалежних змінних розміром п на т (п – число спостережень, т – кількість незалежних змінних); А – вектор параметрів моделі; и – вектор залишків. Нагадаємо передумови застосування 1МНК для оцінки параметрів моделі: 1) математичне сподівання залишків дорівнює нулю, тобто М(u) = 0; (2) 2) значення щ вектора залишків и незалежні між собою і мають постійну дисперсію, тобто M(uu') = де Е – одинична матриця; 3) незалежні змінні моделі не пов'язані із залишками: М(х'u) = 0; (4) 4) незалежні змінні моделі утворюють лінійно незалежну систе Перша умова є очевидною. Адже коли математичне сподівання залишків не дорівнює нулю, то це означає, що існує систематичний вплив на залежну змінну, а до модельної специфікації не введено всіх основних незалежних змінних. Якщо ця передумова не виконується, то йдеться про помилку специфікації. Друга умова передбачає наявність сталої дисперсії залишків. Цю властивість називають гомоскедастичністю. Проте вона може виконуватись лише тоді, коли залишки и є помилками вимірювання. Якщо залишки акумулюють загальний вплив змінних, які не враховані в моделі, то звичайно дисперсія залишків не може бути сталою величиною, вона змінюється для окремих груп спостережень. У такому разі йдеться про явище гетероскедастичності, яке впливає на методи оцінювання параметрів. Третя умова передбачає незалежність між залишками і пояснювальними змінними, яка порушується насамперед тоді, коли еконо-метрична модель будується на базі одночасових структурних рівнянь або має лагові змінні. Тоді для оцінювання параметрів моделі використовуються, як правило, дво- або трикроковий методи найменших квадратів. Четверта умова означає, що всі пояснювальні змінні, які входять до економетричної моделі, мають бути незалежними між собою. Проте очевидно, що в економіці дуже важко вирізнити такий масив незалежних (пояснювальних) змінних, які були б зовсім не пов'язані між собою. Тоді щоразу необхідно з'ясовувати, чи не впливатиме залежність пояснювальних змінних на оцінку параметрів моделі. Це явище називають мультиколінеарністю змінних, що призводить до ненадійності оцінки параметрів моделі, робить їх чутливими до вибраної специфікації моделі та до конкретного набору даних. Знижується рівень довіри до результатів верифікації моделей за допомогою 1МНК. Оцінимо методом 1МНК параметри моделі (1), для якої виконуються умови (2)–(5). Рівняння (1) подамо у вигляді: и = Y-XA. Тоді суму квадратів залишків и можна записати так:
Продиференціюємо цю умову за А і прирівняємо похідні до нуля:
Або X' ХА =Х'Y, (6) де X' – матриця, транспонована до матриці незалежних змінних X. Звідси А = (Х'Х)-1Х'Y. (7) Рівняння (6) дає матричну форму запису системи нормальних рівнянь, а формула (7) показує, що вектор А є розв'язком системи таких рівнянь. Формули (6) і (7) можна одержати й інакше. Так, помноживши рівняння (1) зліва спочатку на X ', а потім на матрицю (X' X)-1, одержимо:
Оскільки (X' X) -1 X' X = Е, то справджується рівність: Згідно з (4), коли п – > ∞, М (X' u) = 0, отже, При цьому значення вектору У цьому випадку числа, що розміщені на її головній діагоналі, характеризують величину дисперсій незалежних змінних, інші елементи відповідають взаємним коваріаціям. Отже, структура матриці моментів відображає зв'язки між незалежними змінними. Чим ближчі показники коваріацій до величини дисперсій, тим ближчий визначник матриці X' X до нуля і тим гірші оцінки параметрів Розглянемо приклад оцінювання параметрів моделі 1МНК. Приклад 1. Оцінити параметри економетричної моделі, що характеризує залежність між тижневими витратами на харчування, загальними витратами та розміром сім'ї. Вихідні дані в умовних одиницях наведені в табл. 1. 1.
Розв'язання Запишемо економетричну модель:
де Оператор оцінювання параметрів моделі за 1МНК має вигляд: А = (Х'Х)-1Х'У,
Де X' – матриця, транспонована до матриці X. Матриця X, крім двох векторів незалежних змінних, містить вектор одиниць. Він дописується в цій матриці ліворуч тоді, коли економетрична модель має вільний член. Не дописуючи такого вектора одиниць, вільний член можна обчислити, скориставшись рівністю:
Згідно з оператором оцінювання знайдемо:
416,2 1601562 23271,2 74,5 23271,2 436,69
2) -0,00017 0,00003 -0,00012 -0,0446 -0,00012 0,0165
Отже, економетрична модель має вигляд: Знайдені методом 1МНК оцінки параметрів такі:
Отже, коли за всіх однакових умов незалежна змінна х, (загальні витрати) збільшується (зменшується) на одиницю, то залежна змінна у (оцінка витрат на харчування) також збільшується (зменшується) на 0,2004 одиниць. Якщо за інших незміннних умов незалежна змінна х2 (розмір сім'ї) збільшується (зменшується) на одиницю, то залежна змінна у (оцінка витрат на харчування) також збільшується (зменшується) на 6,9306 одиниць. У класичній регресійній моделі У = ХА + u; вектор и = (u1, u2,...,un) і залежний від нього вектор У = (у1, у2,…, yn)' є випадковими змінними. До оператора оцінювання Відомо, що для характеристики випадкових змінних
Оцінки коваріаційної матриці використовуються для знаходження стандартних помилок та обчислення довірчих інтервалів оцінок параметрів На головній діагоналі матриці Отже, Де
Оскільки вектор залишків
Звідси маємо альтернативну форму запису дисперсії залишків:
Позначимо (j, k)-й елемент матриці (X' X)-1 символом сjk, тоді j-й елемент по головній діагоналі матриці
Коваріації
Приклад2. Для економетричної моделі обчислимо коваріаційну матрицю
n=16, m= 3 Розв 'язання 1. Обчислимо незміщену оцінку дисперсії залишків
Визначимо дисперсії оцінок
3. Обчислимо коваріації відповідних оцінок параметрів:
Знак «мінус» перед оцінками коваріацій Отже, дістанемо дисперсійно-коваріаційну матрицю
4. Запишемо стандартні помилки оцінок параметрів моделі:
Порівняємо кожну стандартну помилку
Отже, стандартні помилки оцінок параметрів щодо рівня оцінок параметрів становлять відповідно 41 %, 18 % і 12 %, а це свідчить про зміщеність оцінок.
Перевіримо значущість оцінок параметрів Â; і знайдемо для них довірчі інтервали, припустивши для цього, що залишки u нормально розподілені, тобто Перевірку гіпотези виконаємо згідно з t -критерієм:
де Обчислене значення t -критерію порівнюється з табличним при вибраному рівні значущості і На основі t -критерію і стандартної помилки побудуємо довірчі інтервали для параметрів aj:
Перевіримо гіпотези про значущість оцінок параметрів моделі
побудованої на основі вихідних даних, наведених у табл. 1.
Якщо ступінь свободи n – m = 16 – 3 = 13 і рівень значущості Оцінка параметра
Використаємо модель (1) для знаходження прогнозних значень вектора Уо, який відповідатиме очікуваним значенням матриці незалежних змінних Х0.. Наш прогноз може бути точковим або інтервальним. Інтервальний прогноз побудуємо на основі точкового, скориставшись побудованою економетричною моделлю. Щоб отримати інтервальний прогноз, необхідно розрахувати середню похибку прогнозу. Вона зростає з віддаленням значення Розрахуємо спочатку дисперсію прогнозу. У матричному вигляді дисперсія прогнозу
Довірчий інтервал для прогнозних значень
де Зауважимо, що Для визначення інтервального прогнозу індивідуального значення
Отже, інтервальний прогноз індивідуального значення визначається як
. Необхідно розрахувати для економетричної моделі точковий та інтервальний прогнози індивідуального значення залежної змінної, коли для прогнозного періоду відомий вектор
1. Визначаємо точкові прогнозні значення залежної змінної,
Визначаємо дисперсію прогнозу за формулою:
Табличне значення критерію Стьюдента при рівні значущості α= 0,05 і ступенів вільності п - т = 13 дорівнює t0,05 = 2,160. Обчислюємо дисперсію і стандартну помилку прогнозу індивідуального значення у0:
Стандартна помилка прогнозу індивідуального значення у0 така:
Визначаємо інтервальний прогноз індивідуального значення у0:
150,894 - 2,160 ▪ 18,5698 ≤; у0 ≤ 150,894 + 2,160 ▪ 18,5698; 150,894 - 40,111 ≤ у0 ≤ 150,894 + 40,111; 110,783 ≤; у0 ≤ 191,005. Отже, з імовірністю р = 0,95 (α = 0,05) прогноз індивідуального значення у0 потрапляє в інтервал [110,783; 191,005]. Можна також зазначити, що з імовірністю p = 0,95 знайдені прогнози покривають М(у0) і у0 ,коли взяти досить велику кількість вибірок і для кожної з них обчислювати інтервальні прогнози. Економічна інтерпретація: якщо в прогнозному періоді загальні витрати мають рівень 500 одиниць, а сім'я складається з шести осіб, то витрати на харчування потрапляють в інтервал: 110,783 ≤; у0 ≤ 191,005. 6. Багато економічних процесів варто описувати нелінійними залежностями, які бувають двох типів: за змінними і за параметрами. Разом з тим теоретично обґрунтованими і доступними у практичних дослідженнях є лінійні економетричні моделі. Для цілей лінійного регресійного аналізу важливе значення має тільки другий тип лінійності. Нелінійності першого роду за змінними можуть бути легко усунуті шляхом введення нових змінних. Наприклад, якщо обрано поліноміальну модель з однією пояснюючою змінною Y=a0 + a1x + … + amxm + U, z1 =x,…, zm=xm, одержимо множинну лінійну економетричну модель Y=a0 + a1z + … + amzm + U. У випадку поліміальної моделі з декількома пояснюючими змінними Y=a0 + a1x1 + a2x2 + a3x12 + a4x1x2 +a5x22 + …. + U заміна х3 = х12, х4 = х1х2, х5 = х22, … знову приводить до лінійної економетричної моделі. Звичайно рівняння нелінійні за параметрами є нелінійними і за змінними, і їх не можна перетворити у лінійні тільки шляхом уведення нових змінних. Такою є виробнича функція Кобба–Дугласа Y = aF a L b, де Y – обсяг продукції; F – основний капітал; L – робоча сила. Подібні залежності між показником Y і m факторами Z1, Z2, …, Zm записуються у вигляді Y = a0z1a1z2a2…zmameu і за допомогою логарифмічного перетворення lnY = ln a0 + a1ln z1 + a2 ln z2 + … +am ln zm + U зводяться до лінійної за параметрами регресії. Визначення
Призводять до лінійної економетричної моделі Y = a0 + a1 x1 + … + am xm + U. Побудову і аналіз перетвореної лінійної економетричної моделі можна зробити за алгоритмом попередніх розрахунків, які були здійснені саме для лінійної множинної моделі.
Контрольні запитання 1. Дайте означення економетричної моделі. 2. Назвіть етапи побудови економетричної моделі. 3. Що означає специфікація моделі? 4. Коли для оцінки параметрів моделі можна застосувати 1МНК? 5. Запишіть оператор оцінювання 1МНК. Як його можна дістати? 6. Як обчислити матрицю коваріацій параметрів моделей? 7. Запишіть формулу визначення дисперсії залишків. 8. Використовуючи оператор оцінювання 1МНК, знайдіть оцінки параметрів моделі
9. Визначіть вектор коваріації параметрів моделі, базуючись на результатах завдання 8. 14. Порівняйте значення оцінок стандартної помилки. Чи мають зміщення оцінки параметрів? Завдання для самостійної роботи Побудувати множинну лінійної економетричну модель за вихідними даними теми 3 (табл. 1-8), використовуючи лінійний оператор методу найменших квадратів, та проаналізувати її: 1.побудувати дисперсійно-коваріаційну матрицю оцінок параметрів моделі; 2. перевірити знайдені параметри на значущість за критерієм Стьюдента; 3. побудувати інтервали довіри для параметрів моделі; 4.визначити точковий та інтервальний прогнози для Х1прог=17,7, Х2прог=22,8, Х3прог=24,5.
|

 Е, (3)
Е, (3) . (5)
. (5) .
. .
. .Неважко показати, що оцінки
.Неважко показати, що оцінки  , обчислені за (7), мінімізують суму квадратів залишків и.
, обчислені за (7), мінімізують суму квадратів залишків и. є розв'язком так званої системи нормальних рівнянь (Х'Х)
є розв'язком так званої системи нормальних рівнянь (Х'Х) 

 – відповідно фактичні та розрахункові значення тижневих витрат на харчування за моделлю; x1 – загальні витрати; x2 – розмір сім'ї; и – залишки;
– відповідно фактичні та розрахункові значення тижневих витрат на харчування за моделлю; x1 – загальні витрати; x2 – розмір сім'ї; и – залишки;  – оцінка параметрів моделі.
– оцінка параметрів моделі.


 , де
, де  – середнє значення залежної змінної;
– середнє значення залежної змінної;  ,
,  – середні значення незалежних змінних х1, і х2.
– середні значення незалежних змінних х1, і х2.
 1)(Х'Х) = 16 416,2 74,5
1)(Х'Х) = 16 416,2 74,5
 0,314 - 0,00017 -0,0446
0,314 - 0,00017 -0,0446

 .
. ;
;  ;
; 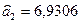 , тобто
, тобто
 , поряд з математичним сподіванням, застосовуються також дисперсія
, поряд з математичним сподіванням, застосовуються також дисперсія  і коваріація
і коваріація  . Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріа-ційну матрицю:
. Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріа-ційну матрицю:

 . Вони використовуються й при перевірці їх статистичної значущості.
. Вони використовуються й при перевірці їх статистичної значущості. містяться оцінки дисперсій
містяться оцінки дисперсій  j- оі оцінки параметрів, що ж до елементів
j- оі оцінки параметрів, що ж до елементів  , які розміщені поза головною діагоналлю, то вони є оцінками коваріації між
, які розміщені поза головною діагоналлю, то вони є оцінками коваріації між  і
і  .
.
 - оцінка дисперсії залишків;
- оцінка дисперсії залишків; .
. , то добуток векторів
, то добуток векторів  можна записати так:
можна записати так: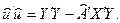
 .
. (8)
(8) , що містяться за межами головної діагоналі, відповідно такі:
, що містяться за межами головної діагоналі, відповідно такі: . (9)
. (9)
 ;
; 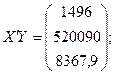
 .
.

 указує на те, що збільшення однієї оцінки параметрів приводить до зменшення в середньому іншої і навпаки.
указує на те, що збільшення однієї оцінки параметрів приводить до зменшення в середньому іншої і навпаки.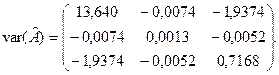 (10)
(10)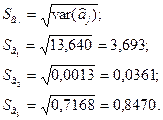
 з відповідним числовим значенням оцінки параметра, тобто знайдемо відношення
з відповідним числовим значенням оцінки параметра, тобто знайдемо відношення  (11):
(11):
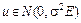 .
. , (12)
, (12)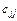 – діагональний елемент матриці
– діагональний елемент матриці  . Знаменник відношення (12)
. Знаменник відношення (12)  – називається стандартною похибкою оцінки параметра моделі.
– називається стандартною похибкою оцінки параметра моделі. ступенях свободи. Якщо t факт >
ступенях свободи. Якщо t факт > . (13)
. (13) ,
, ;
; ;
; .
.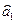 ,
,  ,
, 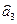 характеризують істотний зв’язок цих незалежних змінних (
характеризують істотний зв’язок цих незалежних змінних ( ,
,  ,
,  ) із залежною.
) із залежною. ;
; ;
; ;
; ;
; ;
;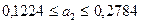 ;
; ;
; ;
; .
. від відповідного середнього значення вибірки.
від відповідного середнього значення вибірки. (14);
(14); (15).
(15). (16)
(16) – критичне значення t-критерію при п - т ступенях вільності і рівні значущості α.
– критичне значення t-критерію при п - т ступенях вільності і рівні значущості α. можна розглядати як точкову оцінку математичного сподівання прогнозного значення
можна розглядати як точкову оцінку математичного сподівання прогнозного значення  , а також як індивідуальне значення
, а також як індивідуальне значення  необхідно знайти відповідну стандартну похибку
необхідно знайти відповідну стандартну похибку  :
: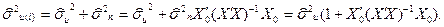
 (17)
(17) .
.

 Стандартна помилка прогнозу:
Стандартна помилка прогнозу: 
 .
.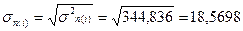 .
. .
. ln Y, a0 = ln a0, x1 = ln z1, …, xm = ln zm
ln Y, a0 = ln a0, x1 = ln z1, …, xm = ln zm , якщо задано вектори Y і X.
, якщо задано вектори Y і X.


