Случайные величины
Случайные величины В результате 10 опытов случайная величина приняла следующие значения: 2,2,3,4,4,4,6,6,6,6. Тогда закон распределения для нее представлен в таблице.
| Случайные величины
 a. 8
b. 9
c. 16
a. 8
b. 9
c. 16
| |||||||||||||||||||||||||||||||
| Математическая статистика Для случайной величины было рассчитано значение дисперсии равное 1,69. Тогда среднеквадратическое отклонение случайной величины равно…. | Математическая статистика При социологическом опросе возрасты его участников(в годах) оказались такими: 28, 52, 53, 45, 38, 31, 35, 28, 29, 21. Чему равен объем выборки? | Математическая статистика При социологическом опросе возрасты его участников(в годах) оказались такими: 20, 25, 21, 22, 20, 19, 20. Чему равно выборочное среднее? | ||||||||||||||||||||||||||||||
| ВАРИАНТ 7 | ВАРИАНТ 8 | ВАРИАНТ 9 | ||||||||||||||||||||||||||||||
| «Основные понятия теории множеств» Определить мощность множества А={6,7,0,*,4,8,3,j,d} a. 3 b. 9 c. 6 | «Основные понятия теории множеств» Выберите такие множества А и В, что А является подмножеством В. a. А=Ø B={1,2,3,4}; b. А={1,2} B={2}; c. А={1,2,3} B={2,3,4}. | «Основные понятия теории множеств»
Известно, что 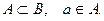 Какие из следующих высказываний верны:
a. Какие из следующих высказываний верны:
a.  b.
b.  c.
c. 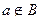
| ||||||||||||||||||||||||||||||
Функции и их свойства
Найти область определения функции
а)  ;
б) ;
б)  . .
| Функции и их свойства
Найти область определения функции
а)  ;
б) ;
б)  . .
| Функции и их свойства
Найти область определения функции
а) 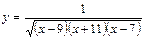 ;
б) ;
б)  . .
| ||||||||||||||||||||||||||||||
| Теория вероятностей Два человека стреляют по одной и той же мишени. Один обычно попадает 8 раз из 10, а второй 7 раз из 10. Вероятность того, что оба попадут в цель после первого выстрела равна …... | Теория вероятностей Игральный кубик бросают один раз. Вероятность того, что на грани выпадет число очков большее 2, равна… | Теория вероятностей Игральный кубик бросают один раз. Вероятность того, что на грани выпадет число очков большее 4, равна…. | ||||||||||||||||||||||||||||||
| Случайные величины Для случайной величины было рассчитано значение среднеквадратического отклонения равное 1,4. Тогда дисперсия случайной величины равна… | Случайные величины
Сумма вероятностей записанных во второй строке закона(таблицы) распределения дискретной случайной величины всегда равна:
| Случайные величины
Дискретная случайная величина х имеет закон распределения вероятностей
| ||||||||||||||||||||||||||||||
Математическая статистика

| Математическая статистика
Выборка задана статистическим рядом
| Математическая статистика
По статистическому распределению выборки установите ее объем
b. 5 c. 23 | ||||||||||||||||||||||||||||||
| ВАРИАНТ 10 | ВАРИАНТ 11 | ВАРИАНТ 12 | ||||||||||||||||||||||||||||||
| «Основные понятия теории множеств» Множество целых чисел является подмножеством множества a. натуральных чисел b. действительных чисел c. пустого множества | «Основные понятия теории множеств»
a. A; b. B; c. C; | «Основные понятия теории множеств»
| ||||||||||||||||||||||||||||||
Функции и их свойства
Найти область определения функции
а)  ;
б) ;
б)  . .
| Функции и их свойства
Найти область определения функции
а)  ;
б) ;
б) 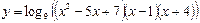 . .
| Функции и их свойства
Найти область определения функции
а)  ;
б) ;
б)  . .
| ||||||||||||||||||||||||||||||
| Теория вероятностей Игральный кубик бросают один раз. Вероятность того, что на грани выпадет число очков большее 6, равна…. | Теория вероятностей Первый завод выпускает качественные станки с вероятностью 0,8. Второй завод выпускает качественные станки с вероятностью 0,9. На каждом заводе купили по одному станку. Какова вероятность того, что оба они качественные… | Теория вероятностей Семена для посадки берут из двух пакетов Вероятность прорастания семян из первого пакета 0,5 из второго 0,8. Какова вероятность, что прорастут семена и из первого и из второго пакетов ….. | ||||||||||||||||||||||||||||||
Случайные величины
Какая из таблиц НЕ МОЖЕТ быть законом распределения дискретной случайной величины?
| Случайные величины
По формуле  считается считается
| Случайные величины Для случайной величины было рассчитано значение среднеквадратического отклонения равное 1,4. Тогда дисперсия случайной величины равна…. | ||||||||||||||||||||||||||||||
| Математическая статистика В результате опытов получена выборка 8, 1, 1, 3, 3, 3, 9, 8. Определите её моду. | Математическая статистика В результате опытов получена выборка -11, 12, -14, 13, -11, 12, -14. Определите её медиану. | Математическая статистика
Статистическое распределение выборки имеет вид
|
I. Подсчет степени обученности учащихся класса, процентного отношения пропущенных уроков к их общему количеству, успеваемости и качества знаний.
1. Запустите редактор электронных таблиц EXCEL. Выделяем ячейки А1до N1, с помощью значка  объединяем ячейки.
объединяем ячейки.

2. В первой строке пишем заголовок «Показатели __________ класса за_______________». Подписываем название столбцов.
3. Создаем виртуальный класс из 10 учащихся, расставляем количество оценок (количество каждой не должно превышать 6 штук), количество пропущенных уроков. Количество предметов 10, всего уроков 120. Выделяем данные и ставим все границы таблицы
4. Находим СОУ – степень обученности учащегося. Вычисляется по формуле СОУ = (число пятерок*1 + число четверок*0,64 + число троек*0,32 + число двоек*0,16)*100 / количество предметов
*- знак умножения, / - знак деления.
В ячейке Н3 строим формулу (буквы латинские) =(C3*1+D3*0,64+E3*0,32+F3*0,16)*100/G3 (после написания формулы нажимаем enter). Затем растягиваем формулу по столбцу.
5. Аналогично считаем общее количество оценок в ячейке I3 =(C3+D3+E3+F3) (после написания формулы нажимаем enter). Затем растягиваем формулу по столбцу.
6. В ячейку L3 записываем формулу подсчета процентного отношения пропущенных уроков к общему их количеству первым учеником =(количество пропущенных уроков / общее количество уроков) * 100%.


 обозначен буквой
обозначен буквой
 обозначен буквой
обозначен буквой


