Расчет болтовых соединений из условия равнопрочности (порядок расчета проиллюстрировать на примере изгибаемыхэлементов)
Стандартные болты, винты шпильки, гайки с крупными шагами спроектированы по условиям равнопрочности, то есть таким образом, что разрушение по любому из видов напряжений может произойти приметно при одной и той же нагрузке на соединение. Это условие позволяет выполнять предварительный (проектный) расчёт соединения в упрощенном варианте. Наиболее часто встречаются три простейшие статически определимые конструктивные схемы (рис. 13.12…13.14). Для схемы (рис. 13.12) с растягивающей рабочей нагрузкой приложенной вдоль продольной оси стержня винта (болта, шпильки) диаметр резьбового стержня по заданному внешнему усилию выбирают по формуле
где F0 – усилие воспринимаемое (передаваемое) резьбовым соединением, d1 – внутренний диаметр резьбовой части стержня, Таблица 13.2
Используя таблицы стандартных резьб по данному внутреннему диаметру и выбранному шагу резьбы можно подобрать необходимый диаметр стержня. Для стержня с крупной резьбой, обращая формулу 13.5, получаем
с последующим округлением результат до ближайшего большего стандартного значения. Если болт поставлен в отверстие с зазором (рис. 13.13) и должен удерживать скрепляемые детали от взаимного поперечного смещения за счёт сил трения, то в этом случае диаметр болта подбирается по формуле
Далее диаметр стержня болта, винта или шпильки определяется аналогично предыдущему варианту. Значение коэффициента трения в формуле (13.13) зависит от множества разных факторов и может меняться в широких пределах (0,06…0,3).
|

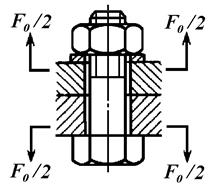 Рис. 13.12. Болтовое соединение, нагруженное растягивающей силой.
Рис. 13.12. Болтовое соединение, нагруженное растягивающей силой.
 Рис. 13.13. Болтовое соединение, нагруженное поперечной силой.
Рис. 13.13. Болтовое соединение, нагруженное поперечной силой.
 ; (13.11)
; (13.11) - допускаемые напряжения для материала стержня при растяжении. Допускаемые напряжения на растяжение для разных сталей принимают в соответствии с табл. 13.2.
- допускаемые напряжения для материала стержня при растяжении. Допускаемые напряжения на растяжение для разных сталей принимают в соответствии с табл. 13.2.
 (13.12)
(13.12) . (13.13)
. (13.13)


