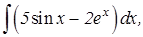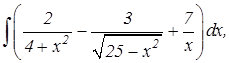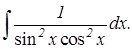Первообразная и неопределенный интеграл
а)
Задание 8.1. Найти интегралы: 1. 3. Определители и матрицы. Системы линейных уравнений 1.1.Матрицы и определители Операции над матрицами. Суммой двух матриц А = (аij) и В = (bij) называется матрица С =(сij), каждый элемент которой равен сумме соответствующих элементов матриц А и В. сij= аi j+ bij i = 1,2, …, m, j =1,2, …, n. Произведением матрицы А = (аij) на число λ; называется матрица λА=(λ аij), где каждый элемент матрицы А умножается на число λ;. Произведением матрицы А = (аi j)mn на матрицу В = (bij)nk называется матрица С =(сij) mk = AB, элемент сij которой равен сумме произведений соответствующих элементов i -ой строки матрицы А и j -ого столбца матрицы В. Важные пределы 1. На основе этого предела существуют следующие эквивалентные бесконечно-малые: При х
2. Пример 1. Пример 2.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Первообразная и неопределенный интеграл Функция F(x) называется первообразной функции f(x) на (a; b), если F'(x) = f(x) для любого Если F(x) и Ф(x) две первообразные функции f(x), то Ф(x) = F(x) + C, т.е. две любые первообразные одной и той же функции отличаются на постоянную величину C. Совокупность всех первообразных F(x) + C функции f(x) называется неопределенным интегралом от функции f(x) и обозначается символом
В равенстве (8.1) f(x) называется подинтегральной функцией, а f(x) dx – подынтегральным выражением. Нахождение неопределенного интеграла по данной подынтегральной функции есть действие интегрирования. Геометрически неопределенный интеграл представляет собой множество плоских кривых y = F(x) + C, которые называют интегральными кривыми. 1. Найти интегралы: а) б) в) г)
|


 2.
2. 

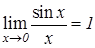 . Первый замечательный предел.
. Первый замечательный предел.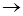 0
0  ,
, или
или 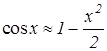 .
.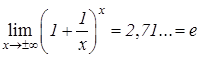 , а также
, а также  . Второй замечательный предел.
. Второй замечательный предел.
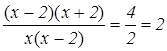 .
.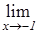
 =
= 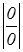 =
= 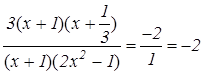 .
. .
.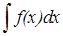 т.е.
т.е. (8.1)
(8.1)