Исходные данные для решения задачи 3
Решение. По условию задачи n = 2, m = 3, т. е. грузовая станция представляет собой многоканальную систему с ограниченной очередью. Интенсивность потока обслуживаний определяется по формуле (4.1): μ =1/2 = 0,5. Интенсивность нагрузки канала (трафик) определяется по формуле (4.2): ρ = 0,4 ∙ 2 = 0,8. Вероятность того, что выгрузочный фронт свободен, определяется по формуле
р0 = 0,431. Вероятность того, что состав будет отправлен на другую станцию, определяется по формуле
ротк = 0,009. Относительная пропускная способность определяется по формуле
Q = 1 – 0,009 = 0,991. Абсолютная пропускная способность определяется по формуле
А = 0,4 ∙ 0,991 = 0,396, т. е. в среднем в сутки разгружается 0,4 состава. Среднее число составов, ожидающих разгрузки, определяется по формуле
где Среднее время ожидания разгрузки определяется по формуле (4.11): Среднее число занятых фронтов (среднее число заявок под обслуживанием) определяется по формуле
Среднее число составов, находящихся у разгрузочного фронта определяется по формуле
Среднее время пребывания состава у разгрузочного фронта определяется по формуле (4.14): Вывод. Среднее время пребывания состава в ожидании разгрузки на другой станции невелико. Это говорит о нормальной работе выгрузочного узла. &Рекомендуемая литература:[1, 2, 4, 5, 8, 9].
|

 об
об
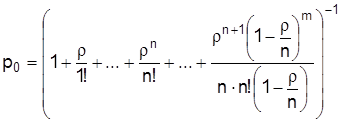 , (4.15)
, (4.15) , (4.16)
, (4.16) , (4.17)
, (4.17) , (4.18)
, (4.18) , (4.19)
, (4.19) = 0,21.
= 0,21. , (4.20)
, (4.20) = 0,77.
= 0,77. , (4.21)
, (4.21) сист = 0,21 + 0,77 = 0,98.
сист = 0,21 + 0,77 = 0,98.


