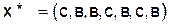ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
6.1. Постановка задачи динамического программирования Динамическое программирование (иначе, динамическое планирование) представляет собой особый математический метод оптимизации решений, специально приспособленный к многошаговым (или многоэтапным) операциям. Для задач динамического программирования универсального метода решения не существует. Одним из основных методов динамического программирования является метод рекуррентных[2] соотношений, который основывается на использовании принципа оптимальности. Принцип оптимальности – каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. На каждом шагу ищется такое управление, которое обеспечивает оптимальное продолжение процесса относительно достигнутого в данный момент состояния. Процесс управления должен быть без обратной связи, т. е. управление на данном шаге не должно оказывать влияния на предшествующие шаги. Экономические задачи, решаемые методами динамического программирования: 1) оптимальная стратегия замены оборудования; 2) оптимальное распределение ресурсов; 3) распределение инвестиций для эффективного использования потенциала предприятия; 4) минимизация затрат на строительство и эксплуатацию предприятий; 5) нахождение рациональных затрат при строительстве трубопроводов и транспортных артерий. Математическая модель задач динамического программирования формулируется следующим образом. Пусть дана операция О, состоящая из m шагов (этапов). Эффективность операции характеризуется показателем «выигрышем» – W. Выигрыш W за всю операцию складывается из выигрышей на отдельных шагах:
где wi – выигрыш на i-м шаге. Если W обладает таким свойством, то его называют аддитивным критерием. Совокупность всех шаговых управлений
Следует иметь в виду, что Требуется найти такое управление х, при котором выигрыш W обращается в максимум:
То управление х*, при котором этот максимум достигается, называется оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений
Формула (6.4) читается так: величина W* есть максимум из всех W(x) при разных управлениях х (максимум берется по всем управлениям х, возможным в данных условиях). 6.2. Пример решения задачи динамического программирования
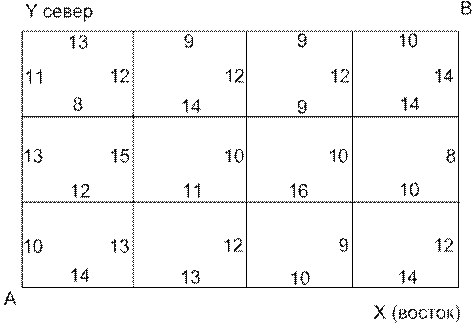
Прокладывается участок железнодорожного пути между пунктами А и В. Требуется так провести дорогу из А в В, чтобы суммарные затраты на сооружение участка были минимальны. Для решения задачи необходимо разделить отрезок АВ на m частей, провести через точки деления прямые, перпендикулярные АВ, и считать за «шаг» переход с одной такой прямой на другую. На каждом шаге можем двигаться либо строго на восток (по оси X), либо строго на север (по оси Y). Тогда путь от А в В представляет ступенчатую ломаную линию, отрезки которой параллельны одной из координатных осей. Затраты на сооружение каждого из отрезков, млн. р., известны (рис. 6.1). Управление всей операцией состоит из совокупности шаговых управлений:
Рис. 6.1. Затраты на сооружение каждого отрезка пути
Разделим расстояние от А до В в восточном направлении на 4 части, в северном – на 3 части. Путь можно рассматривать как управляемую систему, перемещающуюся под влиянием управления из начального состояния А в конечное В. Состояние этой системы перед началом каждого шага будет характеризоваться двумя целочисленными координатами х и у. Для каждого из состояний системы (узловой точки) найдем условное оптимальное управление. Оно выбирается так, чтобы стоимость всех оставшихся шагов до конца процесса была минимальна. Процедуру условной оптимизации проводим в обратном направлении, т. е. от точки В к точке А. Найдем условную оптимизацию последнего шага (рис. 6.2, а).
 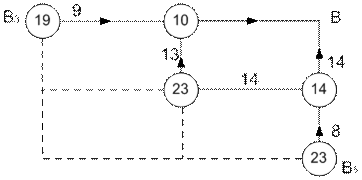
Рис. 6.2. Условная оптимизация шагов решения: а – последний шаг; б – предпоследний шаг
В точку В можно попасть точки из B1 или В2. В узлах записана стоимость пути. Стрелкой показан минимальный путь. Рассмотрим предпоследний шаг (рис. 6.2, б). Для точки В3 условное управление – по оси X, а для точки B5 – по оси Y. Управление для точки В4 выбираем как Условная оптимизация для всех остальных узловых точек показана на рис. 6.3.
Рис. 6.3. Затраты на сооружение каждого отрезка пути Получим Минимальные затраты составляют 10 + 13 + 8 + 12 + 9 + 9 + 10 = = 71 млн. руб. Если решать задачу исходя из оптимальности на каждом этапе, то решение будет следующим: Затраты составят 10 + 12 + 11 + 10 + 9 + 13 + 10 = 75 > 71. Ответ. Прокладывать путь целесообразно по схеме: с, с, в, с, в, в, в, при этом затраты будут минимальные и составят 71 млн. руб. 6.3. Исходные данные
Проложить железнодорожную линию между двумя пунктами А и В так, чтобы суммарные затраты на её постройку были минимальные. Исходные данные по затратам, млн. руб., для проведения расчетов представлены в табл. 6.1, структура сети – на рис. 6.3.
Таблица 6.1
|

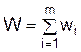 , (6.1)
, (6.1)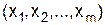 представляет собой управление операцией в целом:
представляет собой управление операцией в целом: . (6.2)
. (6.2) . (6.3)
. (6.3) . (6.4)
. (6.4) , требуется выбрать такое (оптимальное) управление х*, при котором суммарные затраты на сооружение всех участков минимальны:
, требуется выбрать такое (оптимальное) управление х*, при котором суммарные затраты на сооружение всех участков минимальны: 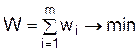 .
.
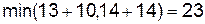 , т. е. по оси Y.
, т. е. по оси Y.
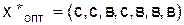 , где с – север, в – восток.
, где с – север, в – восток.