По основным формам тренда
В нашем случае скорректированный коэффициент детерминации принимает максимальное значение по параболическому уравнению тренда, в котором свободным членом b будет число, находящееся в первой строке под данными количества перевезенных пассажиров железнодорожным транспортом, первым зависимым элементом m1 – среднее значение, расположенное под порядковым номером квартала, а вторым зависимым элементом m2 – первое значение строки, находящееся под квадратичными величинами номера квартала. Номер квартала t в этом случае является множителем зависимого числа. Таким образом, уравнение тренда имеет следующий вид:
Подставив в это уравнение значения t = 1, …, 16, найдём уровни Т для каждого момента времени (гр. 5 табл. 7.4). График уравнения тренда приведён на рис. 7.5.
Рис. 7.5. Количество перевезенных пассажиров (фактические, выравненные и полученные по аддитивной модели)
Шаг 5. Найдём значения уровня ряда, полученные по аддитивной модели. Для этого прибавим к уровням Т значения сезонной компоненты для соответствующих кварталов. Графически значения (Т + S) представлены на рис. 7.5. Шаг 6. В соответствии с методикой построения аддитивной модели расчёт ошибки производится по формуле E = Y – (T + S). Это абсолютная ошибка. Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок:
где В нашем случае коэффициент равен 0,696. Это означает, что аддитивная модель на 69,6 % объясняет общую вариацию количества перевезенных пассажиров по кварталам за 4 года. Прогнозирование по аддитивной модели осуществляется в следующем порядке. Предположим, что требуется дать прогноз потребления электроэнергии в течение ближайшего следующего года. Прогнозное значение Ft уровня временного ряда в аддитивной модели в соответствии с соотношением Y = T + S + E есть сумма трендовой и сезонной компонент: Ft = Tt + Si. Для определения трендовой компоненты воспользуемся уравнением тренда, а значения сезонной компоненты были рассчитаны на начальном этапе. Таким образом, прогнозные значения перевезённых пассажиров будут иметь следующий вид:
Значения сезонной компоненты: S1 = –133,07 (I квартал); S2 = 177,96 (II квартал); S3 = 187,08 (III квартал); S4 = –231,97 (IV квартал). Таким образом:
F = 1254,54 + 1567,65 + 1575,7 + 1152,43 = 5550,32. 7.3. Исходные данные
Необходимо рассчитать тренд и спрогнозировать количество перевезенных пассажиров филиалом ОАО «ФПК» на основе наблюдений в течение 10 лет и сделать выводы по результатам табл. 7.5. Таблица 7.5
|


 . (7.2)
. (7.2)
 , (7.3)
, (7.3) – среднее арифметическое количества перевезенных пассажиров.
– среднее арифметическое количества перевезенных пассажиров.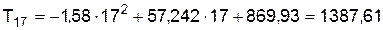 ;
; ;
; ;
; .
. ;
; ;
; ;
; .
.


