Межотраслевой баланс
Во-первых, рассматривая схему баланса по столбцам, можно сделать очевидный вывод, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения
Величина условно чистой продукции Z равна сумме амортизации, оплаты труда и чистого дохода j-й отрасли. Соотношение (8.1) охватывает систему из n уравнений, отражающих стоимостный состав продукции всех отраслей материальной сферы. Во-вторых, рассматривая схему МОБ по строкам для каждой производящей отрасли, можно видеть, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:
Формула (8.2) описывает систему из n уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования. Балансовый характер таблицы выражается в том, что:
Основу экономико-математической модели МОБ составляет матрица коэффициентов прямых материальных затрат А = (аij). Коэффициент прямых материальных затрат аij показывает, какое количество продукции i-й отрасли необходимо, если учитывать только прямые затраты для производства единицы продукции j-й отрасли:
Формула (8.3) предполагает следующие допущения. Первое состоит в том, что сложившуюся технологию производства считаем неизменной. Таким образом, матрица А = (аij) постоянна. Второе состоит в постулировании свойства линейности существующих технологий, т. е. для выпуска j-й отраслью любого объема продукции Xj,-, необходимо затратить продукцию отрасли i в количестве аijXj,-, т. е. материальные издержки пропорциональны объему производимой продукции:
Подставляя выражение (8.4) в балансовое соотношение (8.2), получаем
В матричной форме соотношение (8.5) записывается следующим образом:
С помощью этой модели можно выполнять три вида плановых расчетов. • Задав в модели величины валовой продукции каждой отрасли X,-, можно определить объемы конечной продукции каждой отрасли Y:
• Задав величины конечной продукции всех отраслей Yi, можно определить величины валовой продукции каждой отрасли Xi:
• Для ряда отраслей задав величины валовой продукции, а для всех остальных – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. В формулах (8.7) и (8.8) Е обозначает единичную матрицу n-го порядка, а (E–A)–1 – матрицу, обратную матрице (Е–А). Если определитель матрицы (Е–А) не равен нулю, т. е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим эту обратную матрицу через В = (Е – А)–1, тогда систему уравнений в матричной форме (3.8) можно записать в виде
Элементы матрицы В называются коэффициентами полных материальных затрат. Они показывают, сколько всего нужно произвести продукции n-й отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. Норма больше единицы. Пример решения МОБ. Даны коэффициенты прямых затрат aij и конечный продукт Уi,- для трехотраслевой экономической системы:
Требуется: 1) рассчитать все параметры межотраслевого баланса; 2) заполнить схему межотраслевого баланса. Для решения задачи можно воспользоваться формулой (8.5), которая считается основным математическим соотношением межотраслевого баланса. Для этого составляется и решается соответствующая система линейных уравнений для нахождения объемов валовой продукции по отраслям. После этого вычисляются по приведенным формулам все остальные параметры. Средства EXCEL позволяют организовать вычислительную процедуру более эффективно, решая задачу в матричной форме на основе формулы (8.9). Решение будем осуществлять в окне EXCEL, представленном табл. 8.2. Вначале в ячейки В2:D4 внесем матрицу коэффициентов прямых материальных затрат. Далее рассчитаем величины Е–А. Таблица 8.2
|



 (8.1)
(8.1) (8.2)
(8.2) ;
; .
. , i, j = 1, 2, …, n. (8. 3)
, i, j = 1, 2, …, n. (8. 3) . (8.4)
. (8.4) . (8.5)
. (8.5) . (8.6)
. (8.6) . (8.7)
. (8.7)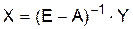 . (8.8)
. (8.8) . (8.9)
. (8.9) ;
;  .
.


