Расчёт оценок сезонной компоненты в аддитивной модели, тыс. чел.
| Номер квартала, t
| Перевезенные пассажиры, 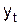
| Итого
за четыре квартала
| Скользящая средняя за
четыре
квартала
| Центрированная
скользящая средняя
| Оценка
сезонной компоненты
| |
|
|
|
|
|
| |
| 846,88
| –
| –
| –
| –
| |
| 1 076,22
| 3847,15
| 961,78
| –
| –
| |
| 1 133,13
| 4014,51
| 1003,62
| 982,70
| 150,42
| |
| 790,92
| 4354,60
| 1088,65
| 1046,14
| –255,22
| |
| 1 014,24
| 4765,19
| 1191,29
| 1139,97
| –125,72
| |
| 1 416,31
| 5039,74
| 1259,93
| 1225,61
| 190,69
| |
| 1 543,72
| 5136,39
| 1284,09
| 1272,01
| 271,70
| |
| 1 065,47
| 5158,50
| 1289,62
| 1286,86
| –221,39
| |
| 1 110,89
| 5020,63
| 1255,15
| 1272,39
| –161,49
| |
| 1 438,42
| 5016,57
| 1254,14
| 1254,65
| 183,77
| |
| 1 405,85
| 5080,93
| 1270,23
| 1262,18
| 143,65
| |
| 1 061,41
| 5128,46
| 1282,11
| 1276,17
| –214,76
| |
| 1 175,26
| 5133,20
| 1283,30
| 1282,70
| –107,45
| |
| 1 485,96
| 5442,83
| 1360,70
| 1322,01
| 163,95
| |
| 1 410,58
| –
| –
| –
| –
| |
| 1 371,04
| –
| –
| –
| –
| В примере показано, что данный временной ряд содержит сезонные колебания с периодичностью 4. Объемы спроса на пассажирские перевозки в осенне-зимний период времени (I и IV кварталы) ниже, чем весной и летом (II и III кварталы). По графику этого ряда (рис. 7.2) можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о соответствии этого ряда аддитивной модели. Рассчитаем ее компоненты.
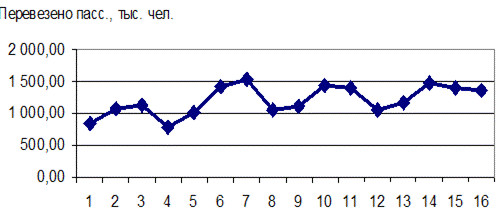
Рис. 7.2. Количество перевезенных пассажиров филиалом за 16 кварталов
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
· просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые значения перевезенных пассажиров (гр. 3 табл. 7.1);
· разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 7.1). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
· приведём эти значения в соответствие с фактическими моментами времени, для чего найдём средние значения из двух последовательно скользящих средних – центрированные скользящие средние (гр. 5 табл. 7.1);
· найдём оценки сезонной компоненты как разность между фактическими уровнями ряда и централизованными скользящими средними (гр. 6 табл. 7.1).
Шаг 2. На этом этапе используем оценки коэффициента детерминации для расчёта сезонной компоненты S. Для этого найдём средние за каждый квартал (по всем годам) оценки сезонной компоненты 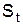 . .
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в равенстве нулю суммы значений сезонной компоненты по всем кварталам. Расчет приведен в табл. 7.2.
Таблица 7.2

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Виды нарушений опорно-двигательного аппарата у детей В общеупотребительном значении нарушение опорно-двигательного аппарата (ОДА) идентифицируется с нарушениями двигательных функций и определенными органическими поражениями (дефектами)...
Особенности массовой коммуникации Развитие средств связи и информации привело к возникновению явления массовой коммуникации...
Тема: Изучение приспособленности организмов к среде обитания Цель:выяснить механизм образования приспособлений к среде обитания и их относительный характер, сделать вывод о том, что приспособленность – результат действия естественного отбора...
|
СИНТАКСИЧЕСКАЯ РАБОТА В СИСТЕМЕ РАЗВИТИЯ РЕЧИ УЧАЩИХСЯ В языке различаются уровни — уровень слова (лексический), уровень словосочетания и предложения (синтаксический) и уровень
Словосочетание в этом смысле может рассматриваться как переходное звено от лексического уровня к синтаксическому...
Плейотропное действие генов. Примеры. Плейотропное действие генов - это зависимость нескольких признаков от одного гена, то есть множественное действие одного гена...
Методика обучения письму и письменной речи на иностранном языке в средней школе. Различают письмо и письменную речь.
Письмо – объект овладения графической и орфографической системами иностранного языка для фиксации языкового и речевого материала...
|
|


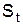 .
.


