Исходные данные для решения задачи 1
Решение. Сортировочную станцию можно рассматривать как одноканальную СМО с неограниченным ожиданием (т. е. с очередью). Таким образом, параметры системы: число каналов n = 1, число мест в очереди m = Интенсивность входящего потока λ = 0,9 состава в час, среднее время обслуживания одной заявки
μ = 1/0,7 = 1,429. Таким образом, нагрузка системы
ρ = 0,9/1,429 = 0,63, или ρ = 0,9 ∙ 0,7 = 0,63. Среднее число составов, ожидающих обслуживания,
Так как ρ < 1, то очередь составов на сортировку не может бесконечно возрастать, значит, предельные вероятности существуют. Вероятность того, что станция свободнаp0, рассчитывается по следующей формуле: pk = ρk(1 – ρ); k = 0,1,2… p0 =1 – ρ.(4.4) p0 = 1 – 0,63 = 0,37, тогда вероятность того, что станция занята pзан = 1 – – 0,37 = 0,63. Среднее число заявок (составов) в системе (на сортировочной станции) рассчитывается по следующей формуле:
где Среднее время пребывания заявки (состава) в очереди (в ожидании сортировки)
Среднее время пребывания заявки (состава) в системе (на сортировочной горке под обслуживанием в ожидании обслуживания)
Вывод. Очевидно, что скорость обслуживания составов на сортировочной станции невысокая, так как время на ожидание обслуживания (1,19 ч) превышает время на обслуживание (0,7 ч). Для повышения эффективности работы сортировочной горки необходимо уменьшить время обслуживания одного состава или увеличить число сортировочных станций. Задача 2. Интенсивность потока пассажиров в кассах железнодорожного вокзала составляет λ = 1,35 чел. в мин. Средняя продолжительность обслуживания кассиром одного пассажира Таблица 4.3
|

 об
об
 .
. , (4.1)
, (4.1) , (4.2)
, (4.2) , (4.3)
, (4.3) оч = 0,632/(1 – 0,63) = 1,073.
оч = 0,632/(1 – 0,63) = 1,073. , (4.5)
, (4.5)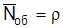 ;
;  , (4.6)
, (4.6) , (4.7)
, (4.7)


