Исходные данные для размещения пунктов отправления и назначения на транспортной сети
Расчет минимальных транспортных затрат между пунктами производства и потребления осуществляется по формуле, руб.,
где е – расходная ставка на 10 ткм. Для рассматриваемого рода груза принимается равной 4 руб.; L – минимальное расстояние, рассчитываемое для заданного полигона между пунктами производства и потребления, км.
2.6. Последовательность решения задачи
Решение задачи осуществляется по вариантам (см. табл. 2.13, 2.14 и 2.16). Расчет вариантов должен быть приведен в работе. Выполнение задачи осуществляется в следующем порядке. 1. Постановка задачи и формулировка экономико-математической модели в соответствии с заданной размерностью. 2. Определение показателей производственных мощностей. Величины мощностей берутся из табл. 2.13, а производственные затраты рассчитываются по формуле (2.10). 3. Расчет затрат на транспортировку единицы запасных частей между пунктами производства и потребления выполняется в следующем порядке: по данным табл. 2.15 строится схема рассматриваемого полигона железных дорог – транспортная сеть, как это показано на фрагменте (рис. 2.6).
Рис. 2.6. Фрагмент транспортной сети
Далее на полученной транспортной сети по соответствующему варианту выделяются узлы, в которых размещены производственные мощности и потребители запасных частей. Затем по сети рассчитываются кратчайшие расстояния между каждым пунктом производства и потребления. Результаты расчета заносятся в таблицу (см. форму табл. 2.11). Затраты на транспортировку рассчитываются по формуле (2.11) в таблице аналогичной формы. 4. Построение расчетной матрицы. Расчетная матрица, соответствующая табл. 2.11, строится на основе подготовленных ранее исходных данных. По существу она представляет собой экономико-математическую модель решаемой задачи в матричной форме. 5. Расчет оптимального плана транспортной задачи для расчетной матрицы. Расчет может быть выполнен без применения вычислительных средств с помощью метода потенциалов (см. подразд. 2.2) или с помощью «Поиска решения» в MS Excel, как это было показано ранее с приложением листинга. Результат решения транспортной задачи оформляется согласно табл. 2.12. Студенты очного отделения решают задачу без применения вычислительных средств (см. подразд. 2.2) и с помощью «Поиска решения» (см. подразд. 2.3). Студенты заочного отделения выбирают способ решения самостоятельно. 6. Расчет показателей оптимального плана загрузки производственных мощностей. Показатели загрузки мощностей по каждому пункту определяются по строкам расчетной матрицы, в которой представлен результат решения транспортной задачи. Загрузка будет равна объему поставок продукции реальным потребителям, т. е. без фиктивного. Далее рассчитываются затраты в целом по оптимальному плану и, в том числе, на производство и транспортировку продукции. 7. Анализ показателей оптимального плана и выводы. 7.1. Сравнить решения, полученные с помощью метода потенциалов и надстройки MS Excel «Поиск решения». 7.2. Оценить долю транспортных затрат. 7.3. Дать рекомендации по размещению пунктов производства и потребления.
& Рекомендуемая литература: [1–7, 9–12].
СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
3.1. Постановка задачи Система методов СПУ – система методов планирования и управления разработкой крупных народно-хозяйственных комплексов, научными исследованиями, конструкторской и технологической подготовкой производства новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов путем применения сетевых графиков. Основу сетевой модели составляет сетевой график – наглядное отображение плана работ. Главными элементами сетевого графика являются события и работы. Событие – состояние, момент достижения промежуточной или конечной цели разработки. Событие не имеет протяжённости во времени. Работа – протяжённый во времени процесс, необходимый для совершения события. События на сетевом графике (или на графе) изображаются кружками (вершинами графа), а работы – стрелками (ориентированными дугами), показывающими связь между работами. При построении сетевого графика необходимо соблюдать ряд правил. 1. В сетевой модели не должно быть «тупиковых» событий, т. е. событий, из которых не выходит ни одна работа, за исключением завершающего события. 2. В сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа. 3. В сети не должно быть замкнутых контуров и петель, т. е. путей соединяющих некоторые события с ними же самими. При возникновении контура необходимо вернуться к исходным данным и путем пересмотра состава работ добиться его устранения 4. Любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. 5. В сети рекомендуется иметь одно исходное и одно завершающее событие. 6. Длина стрелки не зависит от времени выполнения работы. 7. Каждая операция должна быть представлена только одной стрелкой. 8. Следует избегать пересечения стрелок. 9. Не должно быть стрелок, направленных справа налево. 10. Номер начального события должен быть меньше номера конечного события.
3.2. Расчет параметров сетевого графика
3.2.1. Временные параметры сетевых графиков
На рис. 3.1, б изображен пример кодирования работ и событий в принятых обозначениях: tij – продолжительность работы Рi,j, t – ранний срок (ожидаемый момент) осуществления события, t* – поздний срок (предельный момент) осуществления события, n – номер события, nсм – номер предшествующего (смежного) события. На рис. 3.1 в приведён пример изображения события в принятых выше обозначениях. Обозначим через Ранний срок (ожидаемый момент) осуществления j-го события представляет собой момент времени, раньше которого событие произойти не может и рассчитывается по формуле
Поздний срок (предельный момент) осуществления i-го события показывает максимальную задержку во времени наступления данного события:
Одно из важнейших понятий сетевого графика – понятие пути L. Критический путь – последовательность работ между начальными и конечными событиями сети, имеющих наибольшую продолжительность во времени. Минимальное время, необходимое для выполнения проекта, запланированного сетевым графиком, равно длине критического пути. Сетевой график может содержать не один, а несколько критических путей. Критическими называются также работы и события, расположенные на этом пути. Резервный интервал от t до t* для событий, лежащих на критическом пути, равен 0. Для завершающего события сетевого графика поздний срок свершения события должен равняться его раннему сроку, т. е. tп = t*п. Длина критического пути равна раннему сроку свершения завершающего события, т. е. tкр = tп = t*п.
3.2.2. Резервы времени работ Любая из работ пути L на его участке, не совпадающем с критическим путем (замкнутым между двумя событиями критического пути), обладает резервом времени. Среди резервов времени работ наиболее часто используют полный и свободный резервы времени работ. Полный резерв времени
Свободный резерв времени
Работы, лежащие на критическом пути, так же, как и критические события, резервов времени не имеют.
3.3. Сетевой график в условиях неопределённости. Анализ и оптимизация сетевого графика
3.3.1. Сетевое планирование в условиях неопределенности Чаще всего продолжительность работы по сетевому графику заранее не известна и может принимать лишь одно из ряда возможных значений, т. е. продолжительность работы tijявляется случайной величиной, характеризующейся своим законом распределения, а значит, своими числовыми характеристиками – средним значением, или математическим ожиданием, Для определения числовых характеристик а) оптимистическую оценку аij; б) пессимистическую оценку bij; в) наиболее вероятную оценку mij. Указанные три оценки являются основой для расчета средней ожидаемой продолжительности работы ( Предположение о β-распределении продолжительности работы Рi,j позволяет получить следующие оценки ее числовых характеристик:
Общая продолжительность пути L имеет нормальный закон распределения со средним значением
Требуется оценить вероятность того, что срок выполнения проекта tкр не превзойдет заданного директивного срока Т. Полагая tкp случайной величиной, имеющей нормальный закон распределения, получим
где Ф(z) – значение интеграла вероятностей Лапласа, где
где σкр – среднее квадратическое отклонение длины критического пути:
Если P(tкp ≤ Т) мала (например, меньше 0,3), то опасность срыва заданного срока выполнения комплекса велика, необходимо принятие дополнительных мер (перераспределение ресурсов по сети, пересмотр состава работ и событий и т. п.). Если P(tкp ≤ Т) значительна (например, более 0,8), то, очевидно, с достаточной степенью надежности можно прогнозировать выполнение проекта в установленный срок. Значения функции Лапласа определяются с помощью значений таблицы функций Лапласа или с помощью функции «НОРМРАСП» в среде MS Excel (см. подразд. 3.4). 3.3.2. Анализ сетевого графика Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле
где Kсл – коэффициент сложности сетевого графика; nраб – количество работ, ед.; nсоб – количество событий, ед. Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ. Коэффициентом напряженности Кн работы Pi,j называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:
где t(Lmax) – продолжительность максимального пути, проходящего через работу Pi,j , от начала до конца сетевого графика; tкр – продолжительность (длина) критического пути; t'кр – продолжительность отрезка рассматриваемого максимального пути, совпадающего с критическим путем. Коэффициент напряженности Кн работы Pi,j может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности Кн работы Pi,j, тем сложнее выполнить данную работу в установленные сроки. Чем ближе Кн работы Pi,j к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу. Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины Кн выделяют три зоны: критическую (Кн > 0,8); подкритическую (0,6 < Кн < 0,8); резервную (Кн < 0,6).
3.3.3. Оптимизация сетевого графика методом «время-стоимость» При использовании метода «время-стоимость» предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Каждая работа Pi,j характеризуется продолжительностью ti,j, которая может находиться в пределах
где аij – минимально возможная (экстренная) продолжительность работы Pi,j, которую только можно осуществить в условиях разработки; bij – нормальная продолжительность выполнения работы Pi,j. При этом стоимость сi,j работы Pi,j заключена в границах от cmin (при нормальной продолжительности работы) до сmах (при экстренной продолжительности работы). Затраты на ускорение работы Pi,j (по сравнению с нормальной продолжительностью) на единицу времени рассчитываются по формуле
где hi,j – коэффициент затрат на ускорение работы Pi,j. Вариант частной оптимизации сетевого графика с учетом стоимости предполагает использование резервов времени работ. Продолжительность каждой работы, имеющей резерв времени, увеличивают до тех пор, пока не будет исчерпан этот резерв или пока не будет достигнуто верхнее значение продолжительности bij. Стоимость выполнения проекта до оптимизации
Стоимость выполнения проекта после оптимизации уменьшится на величину
Для проведения частной оптимизации сетевого графика, кроме продолжительности работ ti,j, необходимо знать их граничные значения аij и bij, а также показатели затрат на ускорение работ hi,j, вычисляемые по формуле (3.15). Продолжительность каждой работы ti,j целесообразно увеличить в таком размере, чтобы не изменить ранние (ожидаемые) сроки наступления всех событий сети, т. е. на величину свободного резерва времени
3.4. Методика решения задачи
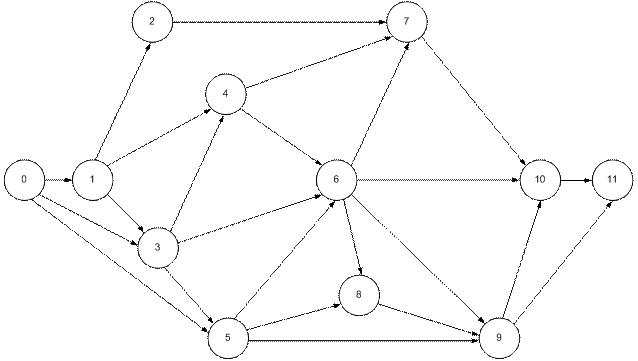
Методику решения задач СПУ рассмотрим на следующем примере. Предположим, что при составлении некоторого проекта выделено 12 событий: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 24 связывающие их работы: (0→1), (0→3), (0→5), (1→2), (1→3), (1→4), (2→7), (3→4), (3→5), (3→6), (4→6), (4→7), (5→6), (5→8), (5→9), (6→7), (6→8), (6→9), (6→10), (7→10), (8→9), (9→10), (9→11), (10→11). Необходимо: 1) составить и упорядочить сетевой график; 2) определить временные параметры сетевого графика; 3) оценить вероятность выполнения проекта в установленный срок; 4) оптимизировать сетевой график методом «время-стоимость». На основании исходных данных был построен и упорядочен сетевой график (рис 3.2).
Рис. 3.2. Сетевой график Каждая работа имеет три временные оценки: оптимистическую, пессимистическую и наиболее вероятную; по формуле (3.5) определяется среднее время выполнения работы (табл. 3.1).
Таблица 3.1
|

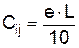 . (2.11)
. (2.11)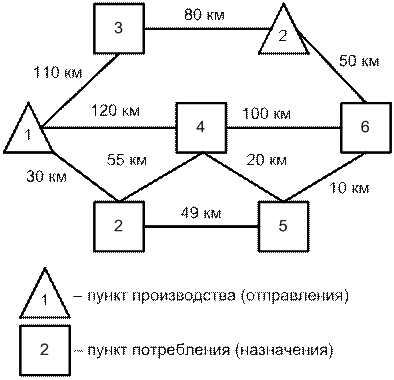
 Начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями. Поэтому для указания конкретной работы используют код работы Рi,j, состоящий из номеров начального (i-го) и конечного (j-го) событий (рис. 3.1, а).
Начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями. Поэтому для указания конкретной работы используют код работы Рi,j, состоящий из номеров начального (i-го) и конечного (j-го) событий (рис. 3.1, а).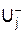 множество работ, входящих в j-е событие, а через
множество работ, входящих в j-е событие, а через  – множество работ, выходящих из i-го события.
– множество работ, выходящих из i-го события. . (3.1)
. (3.1) . (3.2)
. (3.2)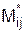 работы Pi,j показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв
работы Pi,j показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв 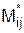 определяется по формуле
определяется по формуле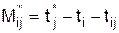 . (3.3)
. (3.3) работы Pi,j представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события.
работы Pi,j представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. 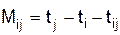 . (3.4)
. (3.4) и дисперсией σ2 i,j.
и дисперсией σ2 i,j. и σ2i,j работы Pi,j на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки:
и σ2i,j работы Pi,j на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки: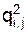 ). При этом используется гипотеза об определенном законе распределения длительностей работ (так называемое β-распределение).
). При этом используется гипотеза об определенном законе распределения длительностей работ (так называемое β-распределение).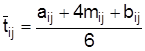 ; (3.5)
; (3.5) . (3.6)
. (3.6) (L), равным сумме средних значений продолжительности составляющих его работ
(L), равным сумме средних значений продолжительности составляющих его работ 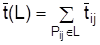 ; (3.7)
; (3.7) . (3.8)
. (3.8) , (3.9)
, (3.9)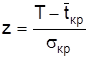 , (3.10)
, (3.10)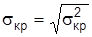 . (3.11)
. (3.11)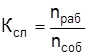 , (3.12)
, (3.12)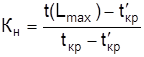 , (3.13)
, (3.13)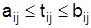 , (3.14)
, (3.14) , (3.15)
, (3.15)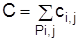 . (3.16)
. (3.16)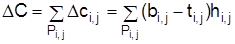 . (3.17)
. (3.17)