Повторение операций 2, 3
От матрицы к матрице грузооборот (затраты на транспортировку) должны снижаться. Если план не оптимален, то необходимо произвести повторный расчёт потенциалов, проверить небазисные клетки на соответствие условию оптимальности. Покажем дальнейшее решение задачи, основываясь на данных табл. 2.6. Результат действий второй и третьей итераций приведен в табл. 2.8. Проверка плана на оптимальность свидетельствует о том, что для двух клеток условия оптимальности не выполняются. После перераспределения поставок по клетке А4В3, получаем новый план (табл. 2.9). Таблица 2.9 Оптимальный план поставок
Проверка плана перевозок на оптимальность по условию (2.8) показала, что для всех небазисных клеток матрицы условия оптимальности выполняются. Функционал F'' оптимального плана равен 1920 ткм. Таким образом, получен план перевозок, обеспечивающий минимальный объем перевозочной работы для транспортировки всего груза между станциями погрузки и выгрузки.
2.3. Решение транспортной задачи линейного программирования с помощью надстройки «Поиск решения» в MS Excel
Рассмотрим последовательность решения предыдущего примера надстройки «Поиск решения» в MS Excel. Вначале вводятся исходные данные (рис. 2.1).
Рис. 2.1. Исходные данные
Расчет ограничений транспортной задачи необходимо выполнять в нижеприведенной последовательности: в ячейки столбика С15:С18 вводим зависимость с помощью функции СУММ Мастера функций. Для этого в соответствующем диалоговом окне вводим адрес строки. На рис. 2.2 представлен адрес для ячейки С15. Аналогичные расчеты следует выполнить для всех пунктов производства и потребления.
Рис. 2.2. Ввод ограничительных уравнений
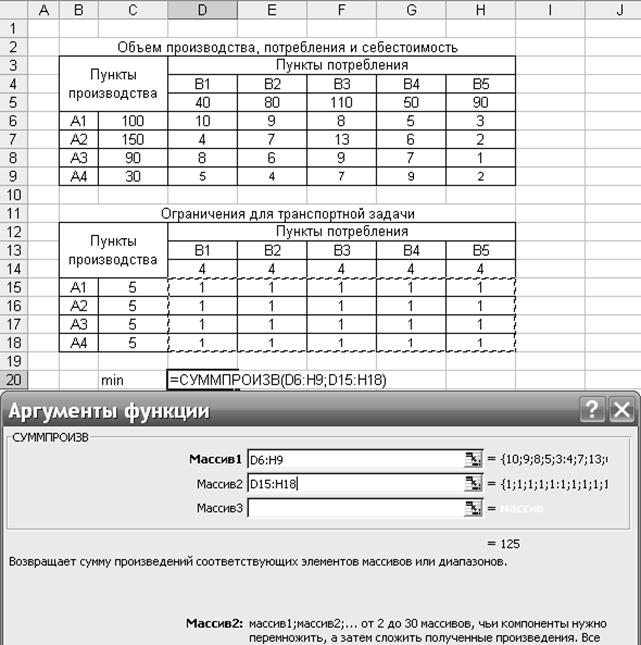
Затем в ячейку D12 вводим целевую функцию (рис. 2.3), представляющую собой сумму произведений себестоимости перевозки тонны груза на один километр и соответственно объем перевозок, условно принятый за единицу по всем пунктам производства и потребления.
Рис. 2.3. Ввод целевой функции
На следующем этапе запускаем «Поиск решения» и заполняем соответствующие ячейки (рис. 2.4.). В поле с единицами располагаются изменяемые ячейки. Следует помнить, что при вводе ограничений должны соблюдаться равенства содержимого ячеек рассчитанных сумм указанным в условии значениям (балансовые ограничения транспортной задачи). Введенные зависимости должны быть равны объему производства и потребления соответственно.
Рис. 2.4. Этап «Поиск решения»
Во вкладке «Параметры» отметить «Линейная модель» и «Неотрицательная значения». Затем нажать «Выполнить» и сохранить полученное значение (рис. 2.5.).
Рис. 2.5. Результаты этапа «Поиск решения»
Как видно из рис. 2.5, функционал (F = 1920 ткм), найденный с помощью метода потенциалов, совпадает со значением целевой функции определённой с помощью надстройки «Поиск решения» в MS Excel.
2.4. Оптимизация загрузки производственных мощностей предприятий по производству запасных частей для железнодорожного транспорта
Железнодорожный транспорт в больших объемах потребляет разнообразные запасные части для поддержания активной части своих производственных фондов в работоспособном состоянии. Запасные части для предприятий железнодорожного транспорта изготавливаются на заводах по ремонту подвижного состава и производству запасных частей и других специализированных предприятиях. Снижение издержек, связанных с обеспечением предприятий железнодорожного транспорта запасными частями весьма актуально. Учитывая большую протяженность железных дорог России, эта задача должна решаться комплексно как для производственной, так и для транспортной составляющей затрат. Для решения этой задачи с успехом может быть использована экономико-математическая модель так называемой транспортной задачи линейного программирования. В частности, ее разновидность – открытая модель транспортной задачи. Для построения экономико-математической модели рассматриваемой задачи введем следующие обозначения: аi – производственные мощности предприятий по производству запасных частей по пунктам размещения i; bj – потребности в запасных частях в пунктах j; xij – объемы перевозок запасных частей между пунктами производства и пунктами потребления i, j; Зi – затраты на производство единицы (удельные затраты) запасных частей у предприятий по пунктам i; сij – затраты на транспортировку единицы запасных частей между пунктами производства и потребления; аi' – загрузка производственных мощностей предприятий по производству запасных частей по пунктам размещения i. Тогда экономико-математическая модель может быть сформулирована следующим образом: найти совокупность переменных аi', минимизирующих целевую функцию F:
В данной задаче предполагается, что суммарная мощность всех предприятий должна превышать общие потребности. Это весьма важно, поскольку при равенстве задача оптимизации теряет смысл, так как будет возможен только один вариант решения при стопроцентной загрузке мощностей. Следовательно, имеет место открытая транспортная задача. Нереализованная продукция относится на счёт фиктивного потребителя. Допустим, имеется три предприятия по производству запасных частей и пять пунктов потребления. Объемы производства будем измерять в тоннах, а затраты в тысячах рублей. Рассмотрим процесс оптимизации на примере. Известны показатели, характеризующие производственные мощности. Они имеют следующие значения: а1 = 500 т; а2 = 400 т; а3 = 700 т; З1= 45 тыс. руб.;З2 = 49 тыс. руб.; З3 = 40 тыс. руб. Потребности в пунктах потребления: b1 = 350 т; b2 = 320 т; b3 = 190 т; b4 = 270 т; b5 = 230 т. Затраты на транспортировку одной тонны запасных частей между пунктами производства и потребления представлены в матрице (табл. 2.10). Таблица 2.10
|







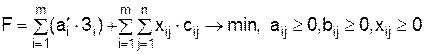 . (2.9)
. (2.9)


