Задание 6. Расчет плоской статически неопределимой рамы методом сил
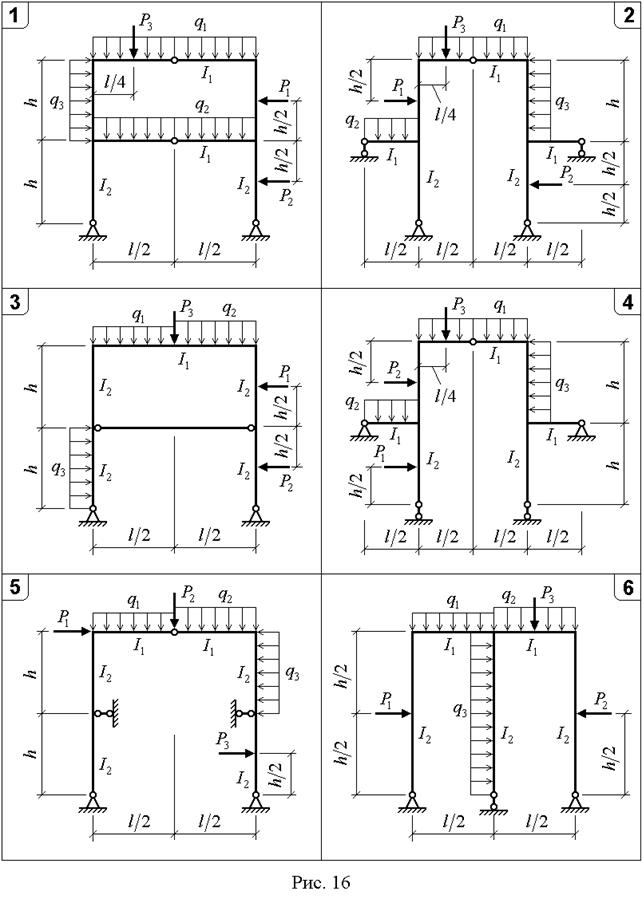
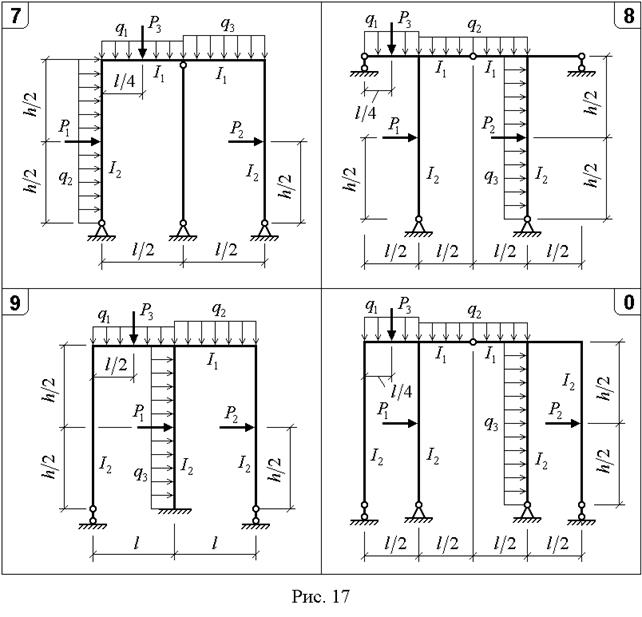
Для статически неопределимой рамы (рис. 16,17) с выбранными по шифру из табл. 10 размерами и нагрузкой требуется:
а) построить эпюры  ;
;
б) выполнить кинематическую проверку.
Таблица 10
| Первая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| P 1, кН
|
|
|
|
|
|
|
|
|
|
|
| P 2, кН
|
|
|
|
|
|
|
|
|
|
|
| P 3, кН
|
|
|
|
|
|
|
|
|
|
|
| l, м
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Вторая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| q 1, кН/м
|
|
|
|
|
|
|
|
|
|
|
| q 2, кН/м
|
|
|
|
|
|
|
|
|
|
|
| q 3, кН/м
|
|
|
|
|
|
|
|
|
|
|
| h, м
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Третья цифра
шифра (№ схемы)
|
|
|
|
|
|
|
|
|
|
|

| 1:2
| 2:3
| 1:3
| 1:3
| 2:3
| 1:3
| 2:1
| 3:2
| 3:4
| 1:2
|
Методические указания. Для расчета статически неопределимой рамы методом сил следует предварительно найти степень статической неопределимости (ССН) и выбрать основную систему (ОС). С целью уменьшения трудоемкости расчета рекомендуется принять симметричную ОС. При построении в ОС единичных и грузовой эпюр необходимо приводить определение опорных реакций. Коэффициенты податливости и свободные члены канонических уравнений метода сил определяются по формулам
 . (6.1)
. (6.1)
Здесь  - изгибающие моменты, возникающие в ОС соответственно от сил
- изгибающие моменты, возникающие в ОС соответственно от сил  и заданной нагрузки;
и заданной нагрузки;  ССН.
ССН.
Для построения окончательных эпюр  необходимо определить реакции опор в ОС с учетом найденных значений сил
необходимо определить реакции опор в ОС с учетом найденных значений сил  и заданной нагрузки и рассчитать ОС как статическую определимую систему.
и заданной нагрузки и рассчитать ОС как статическую определимую систему.
Кинематическая проверка осуществляется по формуле
 . (6.2)
. (6.2)
Интегралы в (6.1) и (6.2) вычисляются либо по правилу Верещагина, либо с помощью соответствующих формул перемножения эпюр (см. методические указания к выполнению задания 4).
Пример выполнения задания. Дано: схема рамы (рис. 18а); 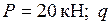
 . Требуется: а) построить эпюры
. Требуется: а) построить эпюры  ; б) выполнить кинематическую проверку.
; б) выполнить кинематическую проверку.
Решение. Находим степень статической неопределимости рамы, которая равна числу ее степеней свободы, взятому с обратным знаком: 
 . Здесь
. Здесь  - число блоков,
- число блоков,  - число простых шарниров,
- число простых шарниров,  - число элементарных опорных связей. Для данной рамы
- число элементарных опорных связей. Для данной рамы  . Отсюда
. Отсюда  . В целях уменьшения трудоемкости расчета выбираем симметричную основную систему (ОС) (рис. 18б). Силу
. В целях уменьшения трудоемкости расчета выбираем симметричную основную систему (ОС) (рис. 18б). Силу  можно приложить к любой части ОС. Неизвестные силы
можно приложить к любой части ОС. Неизвестные силы  и
и 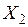 определяются из системы канонических уравнений.
определяются из системы канонических уравнений.

Коэффициенты при неизвестных и свободные члены данных уравнений определяются по формулам (6.1). Для использования данных формул необходимо построить в ОС эпюры  соответственно от сил
соответственно от сил 
 и заданной нагрузки.
и заданной нагрузки.
Определяем реакции опор, возникающие в ОС от силы  :
: 
 . Поскольку выбранная ОС является симметричной, то
. Поскольку выбранная ОС является симметричной, то  . Горизонтальные реакции опор A и B в данном случае отсутствуют, так как все остальные силы действуют вертикально. Находим изгибающие моменты в ОС от силы
. Горизонтальные реакции опор A и B в данном случае отсутствуют, так как все остальные силы действуют вертикально. Находим изгибающие моменты в ОС от силы  .
.
Участки AE и BF:  .
.
Участки DE и KF:  .
.
Участки EC и CF:  .
.
Строим эпюру 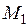 (рис. 18в).
(рис. 18в).
Определяем реакции опор, возникающие в ОС от силы  :
:

 . В силу симметрии ОС
. В силу симметрии ОС  . Определяем изгибающие моменты в ОС от силы
. Определяем изгибающие моменты в ОС от силы  .
.
Участки AE и BF:  .
.
Участки DE и KF:  .
.
Участки EC и CF:  .
.
Строим эпюру  (рис. 18г).
(рис. 18г).
Находим реакции опор, возникающие в ОС от заданной нагрузки (рис. 18д):

Определяем изгибающие моменты в ОС от нагрузки.
Участок AE:  в середине
в середине 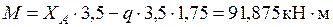 .
.
Участок DE: 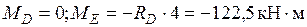 .
.
Участок EC:  .
.
Участок BF:  .
.
Участок CF:  .
.
Участок KF: 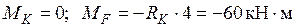 .
.
Строим в ОС эпюру  от нагрузки (рис. 18е).
от нагрузки (рис. 18е).
По эпюрам  определяем коэффициенты при неизвестных и свободные члены канонических уравнений (в соответствии с заданным отношением моментов инерции поперечных сечений ригелей и стоек берем их жесткости на изгиб
определяем коэффициенты при неизвестных и свободные члены канонических уравнений (в соответствии с заданным отношением моментов инерции поперечных сечений ригелей и стоек берем их жесткости на изгиб  ):
):





 .
.
Из канонических уравнений после подстановки в них данных значений получаем  . Для построения эпюр
. Для построения эпюр  находим реакции опор в ОС при совместном действии сил
находим реакции опор в ОС при совместном действии сил  и заданной нагрузки (рис. 19а):
и заданной нагрузки (рис. 19а):



Определяем значения  и
и  на каждом участке.
на каждом участке.
Участок AE: 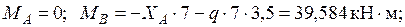 в середине
в середине
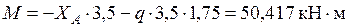 ;
; 
 .
.
Участок DE:  ;
;
 .
.
Участок EC: 
 .
.
Участок BF: 
 .
.
Участок KF: 
 .
.
Участок CF:  ;
;
 .
.
По полученным значениям строим эпюры  (рис. 19б, 19в, 19г).
(рис. 19б, 19в, 19г).
Правильность выполнения расчета устанавливается в результате кинематической проверки, смысл которой состоит в отсутствии перемещений в ОС в направлениях сил  и
и 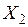 :
:

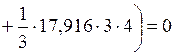 ;
;

 .
.
Для вычисления интегралов использовались формулы (4.2), (4.5).
Задание 7. Расчет неразрезной балки
Для неразрезной балки (рис. 20) с выбранными по шифру из табл. 11 размерами и нагрузкой требуется:
а) построить эпюры  и
и  ;
;
б) выполнить статическую проверку.
Таблица 11
| Первая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| l 1, м
|
|
|
|
|
|
|
|
| 7,5
|
|
| b, м
|
|
|
|
|
|
|
|
|
|
|
| q 1, кН/м
| 1,0
| 1,2
| 1,4
| 1,6
| 1,8
| 1,7
| 1,1
| 1,3
| 1,5
| 1,9
|
|
|
|
|
|
|
|
|
|
|
|
|
| Вторая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| l 2, м
|
|
|
|
|
|
|
|
|
| 7,5
|
| P 1, кН
|
|
|
|
|
|
|
|
|
|
|
| с, м
|
|
|
|
|
|
|
|
|
|
|
| q 2, кН/м
| 1,1
| 1,3
| 0,8
| 1,7
| 1,8
| 1,2
| 0,9
| 1,4
| 1,0
| 1,5
|
|
|
|
|
|
|
|
|
|
|
|
|
| Третья цифра
шифра (№ схемы)
|
|
|
|
|
|
|
|
|
|
|
| l 3, м
|
|
|
|
|
|
|
|
|
|
|
| P 2, кН
|
|
|
|
|
|
|
|
|
|
|

Методические указания. Для расчета неразрезной балки используется метод сил. Наиболее рациональная основная система (ОС) получается путем врезания шарниров над всеми опорами балки кроме крайних. Жесткие заделки заменяются шарнирными неподвижными опорами. Неизвестными обобщенными силами в такой ОС являются опорные моменты  , определяемые из канонических уравнений метода сил. Коэффициенты податливости и свободные члены канонических уравнений определяются по формулам (6.1). Для построения окончательной эпюры изгибающих моментов используется принцип независимости действия сил
, определяемые из канонических уравнений метода сил. Коэффициенты податливости и свободные члены канонических уравнений определяются по формулам (6.1). Для построения окончательной эпюры изгибающих моментов используется принцип независимости действия сил
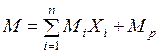 . (7.1)
. (7.1)
Первое слагаемое в (7.1) дает эпюру изгибающих моментов от действия опорных моментов  , которую можно построить откладывая, ординаты
, которую можно построить откладывая, ординаты  в точках приложения этих моментов и соединяя их на каждом пролете балки прямыми линиями. Затем к полученной таким образом эпюре добавляется эпюра
в точках приложения этих моментов и соединяя их на каждом пролете балки прямыми линиями. Затем к полученной таким образом эпюре добавляется эпюра  . Поперечные силы на каждом участке балки определяются по формулам
. Поперечные силы на каждом участке балки определяются по формулам
 , (7.2)
, (7.2)
где  - длина участка;
- длина участка; 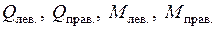 - поперечные силы и изгибающие моменты соответственно на левом и правом концах участка;
- поперечные силы и изгибающие моменты соответственно на левом и правом концах участка;  - интенсивность распределенной нагрузки на рассматриваемом участке. Значения
- интенсивность распределенной нагрузки на рассматриваемом участке. Значения  и
и  в (7.2) берутся положительными, если волокна балки на соответствующих концах участка растянуты с нижней стороны (в этом случае ординаты
в (7.2) берутся положительными, если волокна балки на соответствующих концах участка растянуты с нижней стороны (в этом случае ординаты  и
и  на эпюре
на эпюре 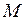 расположены снизу от ее оси). Если на рассматриваемом участке балки
расположены снизу от ее оси). Если на рассматриваемом участке балки  , то из (7.2) получаем постоянную для данного участка поперечную силу
, то из (7.2) получаем постоянную для данного участка поперечную силу
 . (7.3)
. (7.3)
Статическая проверка (проверка равновесия балки) осуществляется двумя уравнениями: 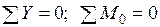 . Необходимые для этого реакции опор определяются по формуле
. Необходимые для этого реакции опор определяются по формуле
 , (7.4)
, (7.4)
где  - поперечные силы соответственно справа и слева от рассматриваемой опоры.
- поперечные силы соответственно справа и слева от рассматриваемой опоры.
Пример выполнения задания. Дано: схема балки (рис. 21а); 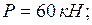
 .
.
Требуется: а) построить эпюры 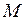 и
и  ; б) выполнить статическую проверку.
; б) выполнить статическую проверку.
Решение. Балка имеет две лишние связи (ССН=2). Для расчета неразрезной балки методом сил выбираем ОС, заменяя заделку неподвижной шарнирной опорой и врезая шарнир над опорой B (рис. 21б). Неизвестные опорные моменты  и
и 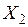 определяются из канонических уравнений
определяются из канонических уравнений

Строим в выбранной ОС эпюры 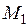 и
и  соответственно от моментов
соответственно от моментов  и
и  (рис. 21в, 21г). Для построения эпюры
(рис. 21в, 21г). Для построения эпюры  рассмотрим участки AB и BCD основной системы как отдельные балки на двух опорах (рис. 21д). На балке AB:
рассмотрим участки AB и BCD основной системы как отдельные балки на двух опорах (рис. 21д). На балке AB: 
 . Для балки BCD предварительно определяем реакции опор:
. Для балки BCD предварительно определяем реакции опор: 
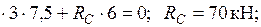
 . После этого находим ординаты эпюры
. После этого находим ординаты эпюры  в характерных сечениях:
в характерных сечениях: 
 . По полученным значениям строим эпюру
. По полученным значениям строим эпюру  (рис. 21е).
(рис. 21е).
Определяем коэффициенты при неизвестных и свободные члены канонических уравнений:





 .
.
Подставляя полученные значения в канонические уравнения, из них находим  , и строим эпюру
, и строим эпюру  от совместного приложения опорных моментов
от совместного приложения опорных моментов  и
и 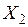 (рис. 21ж). Складывая эту эпюру с эпюрой
(рис. 21ж). Складывая эту эпюру с эпюрой  , получаем эпюру изгибающих моментов в заданной неразрезной балке (рис. 21з).
, получаем эпюру изгибающих моментов в заданной неразрезной балке (рис. 21з).
Поперечные силы на каждом участке определяются по формулам (7.2) и (7.3).

Участок AB:  ;
;
 .
.
Участок BK:  .
.
Участок KC: 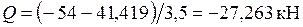 .
.
Участок CD:  ;
;  .
.
По полученным значениям строим эпюру  (рис. 21и). Реакции опор определяются по формуле (7.4):
(рис. 21и). Реакции опор определяются по формуле (7.4): 
 . Реактивный момент определяется непосредственно по эпюре
. Реактивный момент определяется непосредственно по эпюре 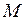 :
:  . Проверяем равновесие балки (рис. 22):
. Проверяем равновесие балки (рис. 22):
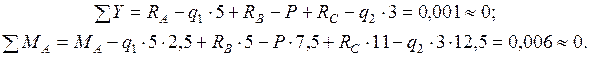

Задание 8. Расчет статически неопределимой фермы
Для статически неопределимой фермы (рис. 23) с выбранными по шифру из табл. 12 размерами и нагрузкой требуется: а) определить силы во всех стержнях; б) выполнить кинематическую проверку.
Методические указания. При расчете статически неопределимой фермы методом сил следует иметь в виду, что при узловом приложении нагрузки в стержнях фермы возникают лишь продольные силы N. Поэтому в общей формуле Мора учитывается только член, содержащий силы N. Так как продольные силы, площади поперечных сечений и модули упругости по длине стержня не меняются, то интегрирование сводится к суммированию:
 . (8.1)
. (8.1)
Здесь  - силы в стержнях ОС соответственно от силы
- силы в стержнях ОС соответственно от силы  и нагрузки;
и нагрузки;  - продольные жесткости и длины стержней. Если ОС получается отбрасыванием какого-либо стержня фермы, то в
- продольные жесткости и длины стержней. Если ОС получается отбрасыванием какого-либо стержня фермы, то в  следует учитывать податливость отброшенного стержня, приняв в нем
следует учитывать податливость отброшенного стержня, приняв в нем  (k - номер отброшенного стержня).
(k - номер отброшенного стержня).
Таблица 12
| Первая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| d, м
| 3,0
| 3,2
| 3,5
| 2,9
| 3,3
| 3,4
| 3,6
| 3,1
| 3,7
| 3,8
|
|
| нижнего пояса
|
| Площади
| F
| 1,2 F
| 1,4 F
| 1,6 F
| 1,8 F
| 1,3 F
| 1,5 F
| 1,7 F
| 1,1 F
| 2 F
|
| сечений
| верхнего пояса
|
|
| 1,5 F
| 1,7 F
| 2 F
| 1,6 F
| 1,4 F
| 1,3 F
| F
| 1,1 F
| 1,2 F
| 1,8 F
|
|
|
|
|
|
|
|
|
|
|
|
|
| Вторая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| P, кН
|
|
|
|
|
|
|
|
|
|
|
|
| решетки
|
| Площади
| 1,2 F
| F
| 2 F
| 0,8 F
| 0,9 F
| 1,3 F
| 1,1 F
| 1,5 F
| 0,7 F
| 1,4 F
|
| сечений
| элементов шпренгеля
|
|
| F
| 1,5 F
| 0,8 F
| 1,1 F
| 0,9 F
| 1,2 F
| 1,3 F
| 1,4 F
| 1,6 F
| 1,7 F
|
|
|
|
|
|
|
|
|
|
|
|
|
| Третья цифра
шифра (№ схемы)
|
|
|
|
|
|
|
|
|
|
|
| h, м
| 3,2
| 3,0
| 3,1
| 2,9
| 3,3
| 3,4
| 3,5
| 3,6
| 3,7
| 3,8
|
Так как модули упругости всех стержней одинаковы и площади  всех сечений выражаются через площадь
всех сечений выражаются через площадь  , то вместо (8.1) удобнее использовать выражения
, то вместо (8.1) удобнее использовать выражения
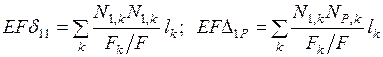 . (8.2)
. (8.2)
Учитывая симметрию, в расчет можно включать только половину фермы. При этом длины стержней, не имеющих парного стержня во второй половине, следует уменьшить вдвое. После подсчета величин  и
и 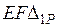 следует определить значение неизвестного:
следует определить значение неизвестного:  . Окончательные значения сил в стержнях фермы определяются по формуле
. Окончательные значения сил в стержнях фермы определяются по формуле 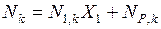 . Для осуществления кинематической проверки используется выражение
. Для осуществления кинематической проверки используется выражение
 . (8.3)
. (8.3)
Все расчеты свести в таблицу.

 Пример выполнения задания
Пример выполнения задания
Дано: схема фермы (рис. 24а); 
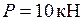 . Площади поперечных сечений стержней фермы: нижнего пояса -
. Площади поперечных сечений стержней фермы: нижнего пояса -  ; верхнего пояса -
; верхнего пояса -  ; решетки -
; решетки -  ; элементов шпренгеля -
; элементов шпренгеля -  . Требуется: а) определить силы во всех стержнях фермы; б) выполнить кинематическую проверку.
. Требуется: а) определить силы во всех стержнях фермы; б) выполнить кинематическую проверку.
Решение. Выбираем симметричную ОС, отбрасывая стержень 11 и заменяя его неизвестной силой  (рис. 24б), определяемой из канонического уравнения
(рис. 24б), определяемой из канонического уравнения  . Коэффициент податливости
. Коэффициент податливости  и свободный член
и свободный член  определяются по формулам
определяются по формулам
 (8.4) Так как модули упругости
(8.4) Так как модули упругости  всех стержней одинаковы и площади поперечных сечений
всех стержней одинаковы и площади поперечных сечений  выражены через площадь
выражены через площадь  , то вместо (8.4) удобнее использовать выражения
, то вместо (8.4) удобнее использовать выражения
 (8.5)
(8.5)
Учитывая, что выбранная ОС является симметричной, суммы в последних выражениях берем только для одной половины, включая стержни 9 и 11, расположенные на оси симметрии (при расчете длины этих стержней уменьшаем вдвое).
Предварительно найдем значения углов  и
и  (рис. 24а), необходимые для дальнейших расчетов:
(рис. 24а), необходимые для дальнейших расчетов:
 .
.
Для определения сил  и
и 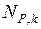 , возникающих в ОС соответственно от сил
, возникающих в ОС соответственно от сил  и заданной нагрузки, используем метод вырезания узлов (в расчетах индексы 1 и P опущены).
и заданной нагрузки, используем метод вырезания узлов (в расчетах индексы 1 и P опущены).
Расчет ОС от сил  . Так как силы
. Так как силы  уравновешены, то реакции опор от этих сил отсутствуют. Вырезаем последовательны узлы ОС (рис. 25) и составляем для них уравнения равновесия.
уравновешены, то реакции опор от этих сил отсутствуют. Вырезаем последовательны узлы ОС (рис. 25) и составляем для них уравнения равновесия.

Узел L: 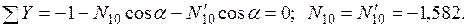
Узел K:  .
.
Узел E: 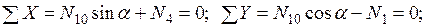
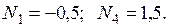
Узел A:  .
.
 .
.
Узел C: 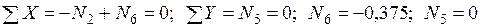 .
.
Узел F: 

 .
.
В стержне 11 от сил 
 .
.
Расчет ОС от нагрузки. Определяем реакции опор: 
 . Из равновесия узлов L, E и K следует:
. Из равновесия узлов L, E и K следует:  .
.

Составляем уравнения равновесия узлов A, C и F (рис. 26).
Узел A: 
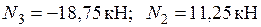 .
.
Узел C: 
 .
.
Узел F: 

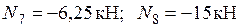 .
.
Вычисляем суммы в правых частях (8.5) Из канонического уравнения находим неизвестную силу:  .
.
Окончательные значения сил  в стержнях фермы определяем по формуле
в стержнях фермы определяем по формуле 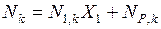 . Расчеты сведены в табл. 13.
. Расчеты сведены в табл. 13.
Таблица 13
| № ст.
| l k
| Fk / F
| N 1, k
| N P,k
| 
| 
| Nk
| 
|
|
| 4,0
| 1,2
| -0,5
| 0,0
| 0,833
| 0,0
| -1,572
| 2,619
|
|
| 3,0
| 1,5
| -0,375
| 11,25
| 0,281
| -8,442
| 10,071
| -7,557
|
|
| 5,0
| 1,2
| 0,625
| -18,75
| 1,627
| -48,809
| -16,875
| -43,928
|
|
| 3,0
| 1,8
| 1,5
| 0,0
| 3,753
| 0,0
| 4,715
| 11,797
|
|
| 4,0
| 1,2
| 0,0
| 10,0
| 0,0
| 0,0
| 10,0
| 0,0
|
|
| 3,0
| 1,5
| -0,375
| 11,25
| 0,281
| -8,442
| 10,071
| -7,557
|
|
| 5,0
| 1,2
| -0,625
| 6,25
| 1,627
| -16,270
| 4,285
| -11,154
|
|
| 3,0
| 1,8
| 0,75
| -15,0
| 0,938
| -18,765
| -12,642
| -15,815
|
|
| 2,0
| 1,2
| 1,0
| 0,0
| 1,667
| 0,0
| 3,144
| 5,238
|
|
| 6,325
| 0,8
| -1,582
| 0,0
| 19,787
| 0,0
| -4,973
| 62,201
|
|
| 1,0
| 0,8
| 1,0
| 0,0
| 1,25
| 0,0
| 3,144
| 3,930
|
| Σ
| -
| -
| -
| -
| 32,043
| -100,728
| -
| -0,226
|
Кинематическая проверка: 
Задание 9. Расчет статически неопределимой рамы методом перемещений
Для заданной статически неопределимой рамы (рис. 27,28) с выбранными по шифру из табл. 14 размерами и нагрузкой требуется: а) построить эпюры  ; б) выполнить статическую проверку.
; б) выполнить статическую проверку.
Таблица 14
| Первая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| l, м
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Вторая цифра
шифра
|
|
|
|
|
|
|
|
|
|
|
| h, м
|
|
|
|
|
|
|
|
|
|
|
| P 1, кН
|
|
|
|
|
|
|
|
|
|
|
| P 2, кН
|
|
|
|
|
|
|
|
|
|
|
| P 3, кН
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Третья цифра
шифра (№ схемы)
|
|
|
|
|
|
|
|
|
|
|

| 1:2
| 2:1
| 2:3
| 3:2
| 1:3
| 3:1
| 3:4
| 4:3
| 4:1
| 1:4
|
Методические указания. Расчет статически неопределимой рамы методом перемещений осуществляется с помощью основной системы (ОС), которая получается из заданной путем введения дополнительных связей, исключающих линейные перемещения и углы поворота узлов (последние вводятся только в жесткие узлы). Для построения в ОС эпюр  от перемещений и углов поворота
от перемещений и углов поворота  , а также эпюры
, а также эпюры  от нагрузки используются справочные данные, приведенные в табл. 15. Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов или частей ОС, содержащих дополнительные связи.
от нагрузки используются справочные данные, приведенные в табл. 15. Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов или частей ОС, содержащих дополнительные связи.
После определения неизвестных  строятся эпюры
строятся эпюры  . Окончательная эпюра изгибающих моментов строится в заданной системе с помощью выражения
. Окончательная эпюра изгибающих моментов строится в заданной системе с помощью выражения  . Эпюра
. Эпюра  на каждом участке строится по эпюре
на каждом участке строится по эпюре  . При отсутствии на участке распределенной нагрузки поперечная сила на нем постоянна и определяется по формуле
. При отсутствии на участке распределенной нагрузки поперечная сила на нем постоянна и определяется по формуле  , где
, где  - изгибающие моменты соответственно на правом (верхнем) и левом (нижнем) концах участка. Моменты
- изгибающие моменты соответственно на правом (верхнем) и левом (нижнем) концах участка. Моменты  подставляются в формулу с учетом их знаков (
подставляются в формулу с учетом их знаков ( растягивает ригели с нижней, стойки - с правой стороны). Продольные силы
растягивает ригели с нижней, стойки - с правой стороны). Продольные силы 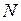 в стержнях определяются по известным значениям
в стержнях определяются по известным значениям  из условий равновесия узлов. При этом
из условий равновесия узлов. При этом  должна поворачивать рассматриваемый узел по часовой стрелке,
должна поворачивать рассматриваемый узел по часовой стрелке, 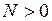 направляется от узла.
направляется от узла.

Проверка равновесия рамы осуществляется тремя уравнениями: 
 (сумму моментов можно составлять относительно любой точки). Необходимые для этого реакции опор определяются из условий равновесия обобщенных внутренних и внешних сил в опорных узлах.
(сумму моментов можно составлять относительно любой точки). Необходимые для этого реакции опор определяются из условий равновесия обобщенных внутренних и внешних сил в опорных узлах.


Пример выполнения задания. Дано: схема рамы (рис. 29а); 
 . Требуется: а) построить эпюры
. Требуется: а) построить эпюры  ; б) выполнить статическую проверку.
; б) выполнить статическую проверку.
Решение. Заданная рама имеет два неизвестных угла поворота жестких узлов и одно неизвестное вертикальное перемещение этих узлов. Основную систему метода перемещений получаем из заданной системы путем введения в нее трех дополнительных связей: двух заделок и одного стержня (рис. 29б). Неизвестные углы поворота  и перемещение
и перемещение  в направлениях дополнительных связей определяются из канонических уравнений
в направлениях дополнительных связей определяются из канонических уравнений


С помощью справочных данных (табл. 15) строим в ОС единичные и грузовую эпюры (рис. 29в, 29г, 29д, 29е). Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов ОС, содержащих дополнительные связи (рис. 30) с учетом заданного отношения  (
( ):
):
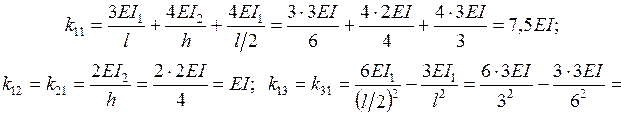


Подставляя эти значения в канонические уравнения и решая последние, получаем:  . Строим в ОС эпюры
. Строим в ОС эпюры  от перемещений
от перемещений  (рис. 31а, 31б, 31в). Окончательная эпюра
(рис. 31а, 31б, 31в). Окончательная эпюра  (рис. 32а) получается с помощью выражения:
(рис. 32а) получается с помощью выражения: 
 . Проверяем равновесие моментов в узле С:
. Проверяем равновесие моментов в узле С: 
 .
.
Поперечные силы на каждом участке определяются по эпюре  .
.
Участок AB:  .
.
Участок BC:  .
.
Участок CD:  .
.
Участок CF: 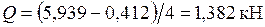 .
.
Участок EF: 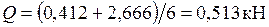 .
.
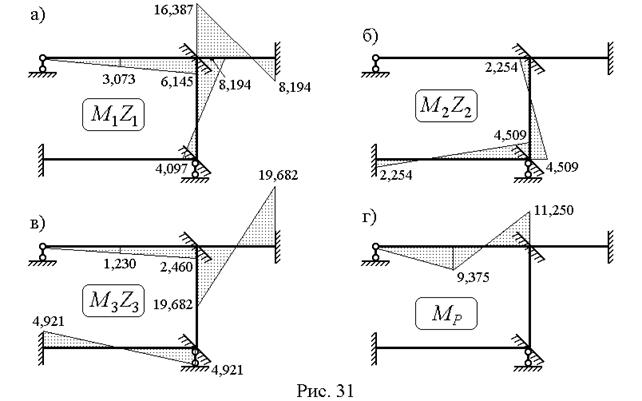
По полученным на участках значениям поперечных сил строим эпюру  (рис.32б).
(рис.32б).
Продольные силы определяем из условия равновесия узлов (рис. 33).
Узел C:  .
.
 .
.
Узел F: 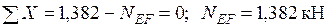 .
.
По полученным значениям строим эпюру 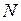 (рис. 32в).
(рис. 32в).
Определяем реакции опор, рассматривая ра

 ;
;


 . (6.1)
. (6.1) - изгибающие моменты, возникающие в ОС соответственно от сил
- изгибающие моменты, возникающие в ОС соответственно от сил  и заданной нагрузки;
и заданной нагрузки;  ССН.
ССН. необходимо определить реакции опор в ОС с учетом найденных значений сил
необходимо определить реакции опор в ОС с учетом найденных значений сил  и заданной нагрузки и рассчитать ОС как статическую определимую систему.
и заданной нагрузки и рассчитать ОС как статическую определимую систему. . (6.2)
. (6.2)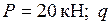
 . Требуется: а) построить эпюры
. Требуется: а) построить эпюры 
 . Здесь
. Здесь  - число блоков,
- число блоков,  - число простых шарниров,
- число простых шарниров,  - число элементарных опорных связей. Для данной рамы
- число элементарных опорных связей. Для данной рамы  . Отсюда
. Отсюда  . В целях уменьшения трудоемкости расчета выбираем симметричную основную систему (ОС) (рис. 18б). Силу
. В целях уменьшения трудоемкости расчета выбираем симметричную основную систему (ОС) (рис. 18б). Силу  можно приложить к любой части ОС. Неизвестные силы
можно приложить к любой части ОС. Неизвестные силы  и
и 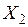 определяются из системы канонических уравнений.
определяются из системы канонических уравнений.
 соответственно от сил
соответственно от сил 
 и заданной нагрузки.
и заданной нагрузки. :
: 
 . Поскольку выбранная ОС является симметричной, то
. Поскольку выбранная ОС является симметричной, то  . Горизонтальные реакции опор A и B в данном случае отсутствуют, так как все остальные силы действуют вертикально. Находим изгибающие моменты в ОС от силы
. Горизонтальные реакции опор A и B в данном случае отсутствуют, так как все остальные силы действуют вертикально. Находим изгибающие моменты в ОС от силы  .
. .
. .
.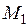 (рис. 18в).
(рис. 18в).
 . В силу симметрии ОС
. В силу симметрии ОС  . Определяем изгибающие моменты в ОС от силы
. Определяем изгибающие моменты в ОС от силы  .
. .
. .
. (рис. 18г).
(рис. 18г).
 в середине
в середине 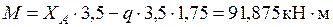 .
.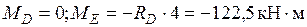 .
. .
. .
. .
.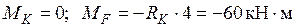 .
. от нагрузки (рис. 18е).
от нагрузки (рис. 18е). ):
):




 .
. . Для построения эпюр
. Для построения эпюр  находим реакции опор в ОС при совместном действии сил
находим реакции опор в ОС при совместном действии сил  и заданной нагрузки (рис. 19а):
и заданной нагрузки (рис. 19а):


 и
и  на каждом участке.
на каждом участке.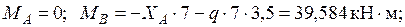 в середине
в середине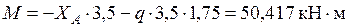 ;
; 
 .
. ;
; .
.
 .
.
 .
.
 .
. ;
; .
.
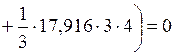 ;
;
 .
. и
и  ;
;
 , определяемые из канонических уравнений метода сил. Коэффициенты податливости и свободные члены канонических уравнений определяются по формулам (6.1). Для построения окончательной эпюры изгибающих моментов используется принцип независимости действия сил
, определяемые из канонических уравнений метода сил. Коэффициенты податливости и свободные члены канонических уравнений определяются по формулам (6.1). Для построения окончательной эпюры изгибающих моментов используется принцип независимости действия сил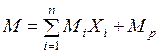 . (7.1)
. (7.1) . Поперечные силы на каждом участке балки определяются по формулам
. Поперечные силы на каждом участке балки определяются по формулам , (7.2)
, (7.2) - длина участка;
- длина участка; 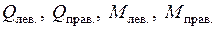 - поперечные силы и изгибающие моменты соответственно на левом и правом концах участка;
- поперечные силы и изгибающие моменты соответственно на левом и правом концах участка;  - интенсивность распределенной нагрузки на рассматриваемом участке. Значения
- интенсивность распределенной нагрузки на рассматриваемом участке. Значения  и
и  в (7.2) берутся положительными, если волокна балки на соответствующих концах участка растянуты с нижней стороны (в этом случае ординаты
в (7.2) берутся положительными, если волокна балки на соответствующих концах участка растянуты с нижней стороны (в этом случае ординаты 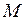 расположены снизу от ее оси). Если на рассматриваемом участке балки
расположены снизу от ее оси). Если на рассматриваемом участке балки  , то из (7.2) получаем постоянную для данного участка поперечную силу
, то из (7.2) получаем постоянную для данного участка поперечную силу . (7.3)
. (7.3)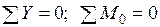 . Необходимые для этого реакции опор определяются по формуле
. Необходимые для этого реакции опор определяются по формуле , (7.4)
, (7.4) - поперечные силы соответственно справа и слева от рассматриваемой опоры.
- поперечные силы соответственно справа и слева от рассматриваемой опоры.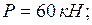
 .
.
 . Для балки BCD предварительно определяем реакции опор:
. Для балки BCD предварительно определяем реакции опор: 
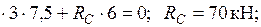
 . После этого находим ординаты эпюры
. После этого находим ординаты эпюры 
 . По полученным значениям строим эпюру
. По полученным значениям строим эпюру 




 .
. , и строим эпюру
, и строим эпюру  от совместного приложения опорных моментов
от совместного приложения опорных моментов 
 ;
; .
. .
.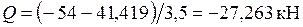 .
. ;
;  .
.
 . Реактивный момент определяется непосредственно по эпюре
. Реактивный момент определяется непосредственно по эпюре  . Проверяем равновесие балки (рис. 22):
. Проверяем равновесие балки (рис. 22):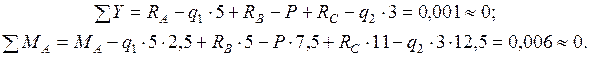

 . (8.1)
. (8.1) - силы в стержнях ОС соответственно от силы
- силы в стержнях ОС соответственно от силы  и нагрузки;
и нагрузки;  - продольные жесткости и длины стержней. Если ОС получается отбрасыванием какого-либо стержня фермы, то в
- продольные жесткости и длины стержней. Если ОС получается отбрасыванием какого-либо стержня фермы, то в  следует учитывать податливость отброшенного стержня, приняв в нем
следует учитывать податливость отброшенного стержня, приняв в нем  (k - номер отброшенного стержня).
(k - номер отброшенного стержня). всех сечений выражаются через площадь
всех сечений выражаются через площадь  , то вместо (8.1) удобнее использовать выражения
, то вместо (8.1) удобнее использовать выражения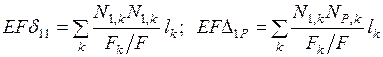 . (8.2)
. (8.2) и
и 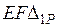 следует определить значение неизвестного:
следует определить значение неизвестного:  . Окончательные значения сил в стержнях фермы определяются по формуле
. Окончательные значения сил в стержнях фермы определяются по формуле 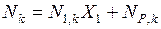 . Для осуществления кинематической проверки используется выражение
. Для осуществления кинематической проверки используется выражение . (8.3)
. (8.3)
 Пример выполнения задания
Пример выполнения задания
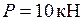 . Площади поперечных сечений стержней фермы: нижнего пояса -
. Площади поперечных сечений стержней фермы: нижнего пояса -  ; верхнего пояса -
; верхнего пояса -  ; решетки -
; решетки -  ; элементов шпренгеля -
; элементов шпренгеля -  . Требуется: а) определить силы во всех стержнях фермы; б) выполнить кинематическую проверку.
. Требуется: а) определить силы во всех стержнях фермы; б) выполнить кинематическую проверку. (рис. 24б), определяемой из канонического уравнения
(рис. 24б), определяемой из канонического уравнения  . Коэффициент податливости
. Коэффициент податливости  определяются по формулам
определяются по формулам (8.4) Так как модули упругости
(8.4) Так как модули упругости  всех стержней одинаковы и площади поперечных сечений
всех стержней одинаковы и площади поперечных сечений  (8.5)
(8.5) и
и  (рис. 24а), необходимые для дальнейших расчетов:
(рис. 24а), необходимые для дальнейших расчетов: .
. и
и 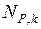 , возникающих в ОС соответственно от сил
, возникающих в ОС соответственно от сил  и заданной нагрузки, используем метод вырезания узлов (в расчетах индексы 1 и P опущены).
и заданной нагрузки, используем метод вырезания узлов (в расчетах индексы 1 и P опущены).
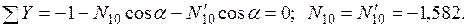
 .
.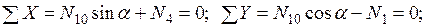
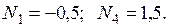
 .
. .
.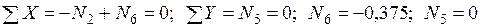 .
.

 .
. .
.
 . Из равновесия узлов L, E и K следует:
. Из равновесия узлов L, E и K следует:  .
.

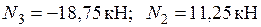 .
.
 .
.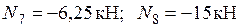 .
. .
. в стержнях фермы определяем по формуле
в стержнях фермы определяем по формуле 



 ; б) выполнить статическую проверку.
; б) выполнить статическую проверку.
 от перемещений и углов поворота
от перемещений и углов поворота  , а также эпюры
, а также эпюры  от нагрузки используются справочные данные, приведенные в табл. 15. Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов или частей ОС, содержащих дополнительные связи.
от нагрузки используются справочные данные, приведенные в табл. 15. Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов или частей ОС, содержащих дополнительные связи. строятся эпюры
строятся эпюры  . Окончательная эпюра изгибающих моментов строится в заданной системе с помощью выражения
. Окончательная эпюра изгибающих моментов строится в заданной системе с помощью выражения  . Эпюра
. Эпюра  на каждом участке строится по эпюре
на каждом участке строится по эпюре  . При отсутствии на участке распределенной нагрузки поперечная сила на нем постоянна и определяется по формуле
. При отсутствии на участке распределенной нагрузки поперечная сила на нем постоянна и определяется по формуле  , где
, где  - изгибающие моменты соответственно на правом (верхнем) и левом (нижнем) концах участка. Моменты
- изгибающие моменты соответственно на правом (верхнем) и левом (нижнем) концах участка. Моменты  подставляются в формулу с учетом их знаков (
подставляются в формулу с учетом их знаков ( растягивает ригели с нижней, стойки - с правой стороны). Продольные силы
растягивает ригели с нижней, стойки - с правой стороны). Продольные силы 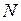 в стержнях определяются по известным значениям
в стержнях определяются по известным значениям  должна поворачивать рассматриваемый узел по часовой стрелке,
должна поворачивать рассматриваемый узел по часовой стрелке, 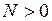 направляется от узла.
направляется от узла.

 (сумму моментов можно составлять относительно любой точки). Необходимые для этого реакции опор определяются из условий равновесия обобщенных внутренних и внешних сил в опорных узлах.
(сумму моментов можно составлять относительно любой точки). Необходимые для этого реакции опор определяются из условий равновесия обобщенных внутренних и внешних сил в опорных узлах.


 . Требуется: а) построить эпюры
. Требуется: а) построить эпюры  и перемещение
и перемещение  в направлениях дополнительных связей определяются из канонических уравнений
в направлениях дополнительных связей определяются из канонических уравнений

 (
( ):
):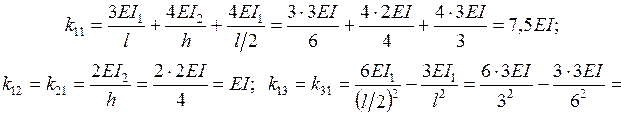


 . Строим в ОС эпюры
. Строим в ОС эпюры  от перемещений
от перемещений 
 . Проверяем равновесие моментов в узле С:
. Проверяем равновесие моментов в узле С: 
 .
. .
. .
. .
.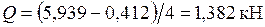 .
.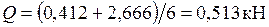 .
.
 .
. .
.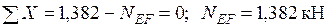 .
.


