Решение. Результаты перечета деревьев на пробных площадях, их диаметр, порода, визуальная (качественная) классификация по категориям состояния – указаны в таблицах
Результаты перечета деревьев на пробных площадях, их диаметр, порода, визуальная (качественная) классификация по категориям состояния – указаны в таблицах А.1- А.4. Знаком * отмечены деревья, которые оценивались по диэлектрическим характеристикам. Таблица А.1 – Пробная площадь № 1
Решение. 1. Построим поле корреляции:
Уже исходя из графика видно, что значения
Теперь вычисляем коэффициент автокорреляции первого порядка:
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка.
Следовательно, Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу 3.
Коррелограмма:
Анализ коэффициентов автокорреляции позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
2. Построение аддитивной модели временного ряда. Было показано, что данный временной ряд содержит сезонные колебания периодичностью 4, т.к. количество правонарушений в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда. I этап. Расчет сезонной компоненты Расчет оценок 1. Просуммируем данные за каждые 4 квартала (т.к. 2. Разделим полученные значения на 4 (осреднение), получим выровненные значения, которые не содержат сезонной компоненты (столбец 4). 3. Приведем эти значения к фактическому моменту времени. Для этого найдем среднее значение двух соседних скользящих средних — центрированных скользящих средних (столбец 5). 4. Найдем оценки сезонной компоненты
5. Используем эти оценки для расчета значений сезонной компоненты
В моделях с сезонной компонентой предполагается, что сезонные воздействия за период
В задаче: 0,550 – 1,938 – 1,275 + 2,663 = 0,016 Чтобы устранить эту погрешность вводится корректирующий коэффициент
Скорректированные по формуле
II этап. Построение линии регрессии для величины Аналитическое выравнивание трендовой составляющей 1. Вычтем значение сезонной компоненты
2. Построим уравнение линейной регрессии для составляющей
Выбор уравнения линейной регрессии объясняется диаграммой рассеяния величины
Параметры
Окончательно: 3. По найденному уравнению рассчитываем теоретические значения
4. Находим теоретические значения потребления электроэнергии по кварталам (столбец 6)
На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели:
III этап. Расчет ошибок аддитивной модели. 1. По каждому уравнению рассчитываем абсолютную ошибку (столбец 7)
2. Находим остаточную дисперсию (столбец 8)
3. Находим общую дисперсию (столбец 9)
4. Вычисляем индекс детерминации
Следовательно, можно сказать, что аддитивная модель объясняет 97,8% общей вариации уровней временного ряда потребления электроэнергии жителями региона по кварталам за 4 года.
IV этап. Проверка адекватности модели данным наблюдения.
Поскольку
3. Прогнозирование на два квартала вперед. Для определения трендовой компоненты воспользуемся уравнением тренда:
Получим:
Значения сезонных компонент за соответствующие кварталы равны:
Таким образом:
|
образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу.
.
методом скользящей средней.
) со сдвигом на один шаг по времени и определим условные годовые объемы потребления электроэнергии (столбец 3).
по кварталам:
:
значения (указаны в последней строке таблицы) являются значениями сезонной компоненты по кварталам.
.
будем осуществлять по шагам, заполняя каждый раз таблицу 6.
из соответствующего уровня временного ряда 
(столбец 4)
:
определяются МНК:
.
(столбец 5).
; 
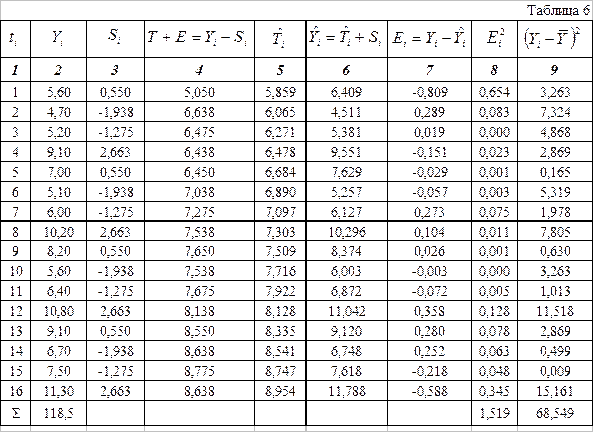
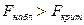, то уравнение значимо.
; 
; 
; 
