Аксиомы принадлежности.
Обозначим множество точек через М, множество прямых через L, а множество плоскостей через P. На декартовых произведениях  и
и  введем бинарные отношения
введем бинарные отношения 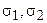 и
и  , которые будем называть отношениями принадлежности. Если точка А и прямая l находятся в отношении
, которые будем называть отношениями принадлежности. Если точка А и прямая l находятся в отношении 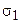 , т.е. пара (А, l) Î
, т.е. пара (А, l) Î 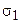 , то будем говорить, что точка А принадлежит или лежит на прямой l, или, что то же самое, прямая l проходит через точку А или ее содержит. Аналогично, если А – точка, а p - плоскость и
, то будем говорить, что точка А принадлежит или лежит на прямой l, или, что то же самое, прямая l проходит через точку А или ее содержит. Аналогично, если А – точка, а p - плоскость и  , то будем использовать следующую терминологию: точка принадлежит плоскости, точка лежит на плоскости, плоскость содержит точку или плоскости проходит через эту точку. В случае, когда прямая l и плоскость p находятся в отношении
, то будем использовать следующую терминологию: точка принадлежит плоскости, точка лежит на плоскости, плоскость содержит точку или плоскости проходит через эту точку. В случае, когда прямая l и плоскость p находятся в отношении  , т.е.
, т.е.  , то будем говорить: прямая лежит, принадлежит или содержится в плоскости, а плоскость содержит или проходит через эту прямую. Точки, прямые и плоскости должны удовлетворять следующим аксиомам.
, то будем говорить: прямая лежит, принадлежит или содержится в плоскости, а плоскость содержит или проходит через эту прямую. Точки, прямые и плоскости должны удовлетворять следующим аксиомам.
 . Каковы бы ни были две точки А и В, существует прямая а, проходящая через эти две точки.
. Каковы бы ни были две точки А и В, существует прямая а, проходящая через эти две точки.
 . Каковы бы ни были две точки А и В, существует не более одной прямой а, проходящей через эти две точки.
. Каковы бы ни были две точки А и В, существует не более одной прямой а, проходящей через эти две точки.
 . На каждой прямой лежит, по крайней мере, две точки. Существует, по крайней мере, три точки, не принадлежащие одной прямой.
. На каждой прямой лежит, по крайней мере, две точки. Существует, по крайней мере, три точки, не принадлежащие одной прямой.
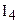 . Каковы бы ни были три точки А.В и С, не лежащие на одной прямой, существует плоскость a, проходящая через эти три точки. На каждой плоскости лежит, по крайней мере, одна точка.
. Каковы бы ни были три точки А.В и С, не лежащие на одной прямой, существует плоскость a, проходящая через эти три точки. На каждой плоскости лежит, по крайней мере, одна точка.
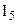 . Каковы бы ни были три точки, не лежащие на одной прямой, существует не более одной плоскости, содержащей эти точки.
. Каковы бы ни были три точки, не лежащие на одной прямой, существует не более одной плоскости, содержащей эти точки.
 . Если две точки А и В прямой а лежат в плоскости a, то любая точка, принадлежащая прямой а, принадлежит плоскости a.
. Если две точки А и В прямой а лежат в плоскости a, то любая точка, принадлежащая прямой а, принадлежит плоскости a.
 . Если две плоскости a и b имеют общую точку А, то существует, по крайней мере, еще одна В, принадлежащая этим плоскостям.
. Если две плоскости a и b имеют общую точку А, то существует, по крайней мере, еще одна В, принадлежащая этим плоскостям.
 . Существует, по крайней мере, четыре точки, не лежащие в одной плоскости.
. Существует, по крайней мере, четыре точки, не лежащие в одной плоскости.
10. Две прямые имеют не более одной точки.
20. Если две плоскости имеют общую точку, то они имеют общую прямую.
30. Через прямую и не лежащую на ней точку проходит одна и только одна плоскость.
40. Через две пересекающиеся прямые проходит одна и только одна плоскость.
50. На каждой плоскости существует три точки, не лежащие на одной прямой.
Заметим, что из аксиом первой группы не следует, что множество основных элементов, точек, прямых и плоскостей, бесконечно. Рассмотрим модель, доказывающую это утверждение. Пусть дано множество, состоящее из четырех элементов: A, B, С и D. Для наглядности расположим их в вершинах тетраэдра (рис. 5). Под точками будем пони  мать элементы A, B, С и D (вершины тетраэдра), под прямыми – неупорядоченные пары элементов AB, AC, AD, BC, BD и CD (ребра тетраэдра), а под плоскостями - неупорядоченные тройки этих элементов ABC, ABD, ACD и BCD (грани тетраэдра). Точка принадлежит прямой или плоскости, если она входит в соответствующую пару или тройку точек, а прямая принадлежит плоскости, если она как пара точек входит в тройку точек, определяющую плоскость. Выполнение требований аксиом
мать элементы A, B, С и D (вершины тетраэдра), под прямыми – неупорядоченные пары элементов AB, AC, AD, BC, BD и CD (ребра тетраэдра), а под плоскостями - неупорядоченные тройки этих элементов ABC, ABD, ACD и BCD (грани тетраэдра). Точка принадлежит прямой или плоскости, если она входит в соответствующую пару или тройку точек, а прямая принадлежит плоскости, если она как пара точек входит в тройку точек, определяющую плоскость. Выполнение требований аксиом  проверяется достаточно просто. Например, рассмотрим требование аксиомы
проверяется достаточно просто. Например, рассмотрим требование аксиомы  . Очевидно, оно выполняется, так как в тетраэдре если две грани имеют общую вершину, то они пересекаются по ребру, т.е. имеют еще одну общую вершину. Выполнение остальных аксиом проверьте самостоятельно.
. Очевидно, оно выполняется, так как в тетраэдре если две грани имеют общую вершину, то они пересекаются по ребру, т.е. имеют еще одну общую вершину. Выполнение остальных аксиом проверьте самостоятельно.

 и
и  введем бинарные отношения
введем бинарные отношения 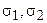 и
и  , которые будем называть отношениями принадлежности. Если точка А и прямая l находятся в отношении
, которые будем называть отношениями принадлежности. Если точка А и прямая l находятся в отношении 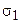 , т.е. пара (А, l) Î
, т.е. пара (А, l) Î  , то будем использовать следующую терминологию: точка принадлежит плоскости, точка лежит на плоскости, плоскость содержит точку или плоскости проходит через эту точку. В случае, когда прямая l и плоскость p находятся в отношении
, то будем использовать следующую терминологию: точка принадлежит плоскости, точка лежит на плоскости, плоскость содержит точку или плоскости проходит через эту точку. В случае, когда прямая l и плоскость p находятся в отношении  , то будем говорить: прямая лежит, принадлежит или содержится в плоскости, а плоскость содержит или проходит через эту прямую. Точки, прямые и плоскости должны удовлетворять следующим аксиомам.
, то будем говорить: прямая лежит, принадлежит или содержится в плоскости, а плоскость содержит или проходит через эту прямую. Точки, прямые и плоскости должны удовлетворять следующим аксиомам. . Каковы бы ни были две точки А и В, существует прямая а, проходящая через эти две точки.
. Каковы бы ни были две точки А и В, существует прямая а, проходящая через эти две точки. . Каковы бы ни были две точки А и В, существует не более одной прямой а, проходящей через эти две точки.
. Каковы бы ни были две точки А и В, существует не более одной прямой а, проходящей через эти две точки. . На каждой прямой лежит, по крайней мере, две точки. Существует, по крайней мере, три точки, не принадлежащие одной прямой.
. На каждой прямой лежит, по крайней мере, две точки. Существует, по крайней мере, три точки, не принадлежащие одной прямой.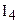 . Каковы бы ни были три точки А.В и С, не лежащие на одной прямой, существует плоскость a, проходящая через эти три точки. На каждой плоскости лежит, по крайней мере, одна точка.
. Каковы бы ни были три точки А.В и С, не лежащие на одной прямой, существует плоскость a, проходящая через эти три точки. На каждой плоскости лежит, по крайней мере, одна точка. . Каковы бы ни были три точки, не лежащие на одной прямой, существует не более одной плоскости, содержащей эти точки.
. Каковы бы ни были три точки, не лежащие на одной прямой, существует не более одной плоскости, содержащей эти точки. . Если две точки А и В прямой а лежат в плоскости a, то любая точка, принадлежащая прямой а, принадлежит плоскости a.
. Если две точки А и В прямой а лежат в плоскости a, то любая точка, принадлежащая прямой а, принадлежит плоскости a. . Если две плоскости a и b имеют общую точку А, то существует, по крайней мере, еще одна В, принадлежащая этим плоскостям.
. Если две плоскости a и b имеют общую точку А, то существует, по крайней мере, еще одна В, принадлежащая этим плоскостям. . Существует, по крайней мере, четыре точки, не лежащие в одной плоскости.
. Существует, по крайней мере, четыре точки, не лежащие в одной плоскости. мать элементы A, B, С и D (вершины тетраэдра), под прямыми – неупорядоченные пары элементов AB, AC, AD, BC, BD и CD (ребра тетраэдра), а под плоскостями - неупорядоченные тройки этих элементов ABC, ABD, ACD и BCD (грани тетраэдра). Точка принадлежит прямой или плоскости, если она входит в соответствующую пару или тройку точек, а прямая принадлежит плоскости, если она как пара точек входит в тройку точек, определяющую плоскость. Выполнение требований аксиом
мать элементы A, B, С и D (вершины тетраэдра), под прямыми – неупорядоченные пары элементов AB, AC, AD, BC, BD и CD (ребра тетраэдра), а под плоскостями - неупорядоченные тройки этих элементов ABC, ABD, ACD и BCD (грани тетраэдра). Точка принадлежит прямой или плоскости, если она входит в соответствующую пару или тройку точек, а прямая принадлежит плоскости, если она как пара точек входит в тройку точек, определяющую плоскость. Выполнение требований аксиом  проверяется достаточно просто. Например, рассмотрим требование аксиомы
проверяется достаточно просто. Например, рассмотрим требование аксиомы 


