Аксиомы порядка
На декартовом произведении
Для формулировки последней, четвертой аксиомы второй группы удобно ввести следующие понятие. Определение 3.1. Под отрезком (по Гильберту) будем понимать пару точек АВ. Точки А и В будем называть концами отрезка, точки, лежащие между его концами – внутренними точками отрезка, или просто точками отрезка, а точки прямой АВ, не лежащими между концами А и В – внешними точками отрезка.
Из аксиом первой и второй групп вытекает достаточно много геометрических свойств точек, прямых и отрезков. Можно доказать, что любой отрезок имеет, по крайней мере, одну внутреннюю точку, среди трех точек прямой всегда существует одна и только одна, лежащая между двумя другими, между двумя точками прямой всегда существует бесконечно много точек, что означает на прямой существует бесконечно много точек. Можно также доказать, что утверждение аксиомы Паша справедливо и для точек, лежащих на одной прямой: если точки А, В и С принадлежат одной прямой, прямая l не проходи через эти точки и пересекает один из отрезков, например, АВ в внутренней точке, то она пересекает во внутренней точке либо отрезок АС, либо отрезок ВС. Заметим также, что из аксиом первой и второй групп не следует, что множество точек прямой несчетно. Мы не будем приводить доказательства этих утверждений. Читатель может познакомиться с ними в пособиях [6], [7] и [8]. Остановимся более подробно на основных геометрических понятиях, а именно луча, полуплоскости и полупространства, которые вводятся с помощью аксиом принадлежности и порядка. Справедливо следующее утверждение: Точка О прямой l разбивает множество остальных точек этой прямой на два непустых подмножества так, что для любых двух точек А и В, принадлежащих одному подмножеству, точка О является внешней точкой отрезка АВ, а для любых двух точек C и D, принадлежащих различным подмножествам, точка О – внутренняя точка отрезка CD. Каждое из этих подмножеств называется лучом прямой l с началом в точке О. Лучи будем обозначать через h, l, k, …OA, OB, OC,…, где О – начало луча, а А, В и С – точки луча. Доказательство этого утверждения мы приведем позже, в параграфе 7, но используя при этом другую аксиоматику трехмерного евклидова пространства. Понятие луча позволяет определить важнейший геометрический объект – угол. Определение 3.2. Под углом (по Гильберту) будем понимать пару лучей h и k, имеющих общее начало О и не лежащих на одной прямой. Точка О называется вершиной угла, а лучи h и k – его сторонами. Для углов будем использовать обозначения Теорема 3.1. Прямая а, лежащая в плоскости a, разделяет ее множество точек, не принадлежащих прямой, на два непустых подмножества, так, что если точки А и В принадлежат одному подмножеству, то отрезок АВ не имеет общих точек с прямой l, а если точки А и В принадлежат различным подмножествам, то отрезок АВ пересекает прямую l в своей внутренней точке. Доказательство. При доказательстве мы будем использовать следующее свойство отношения эквивалентности. Если на некотором множестве введено бинарное отношение, которое является отношением эквивалентности, т.е. удовлетворяет условиям рефлексивности, симметричности и транзитивности, то все множество разбивается на непересекающиеся подмножества - классы эквивалентности, при этом любые два элемента принадлежат одному классу в том и только в том случае, когда они эквивалентны. Рассмотрим множество точек плоскости, не принадлежащих прямой а. Будем считать, что два точки А и В находятся в бинарном отношении d: АdВ в том и только в том случае, когда на отрезке АВ не существует внутренних точек, принадлежащих прямой а. Будем также счи Докажем, что отношение d является отношением эквивалентности. Условие рефлексивности с очевидностью выполняется в силу определения бинарного отношения d: АdА. Пусть точки А и В находятся в отношении d. Тогда на отрезке АВ не существует точек прямой а. Отсюда следует, что точек прямой а нет и на отрезке ВА, поэтому ВdА, отношение симметричности выполнено. Пусть, наконец, даны три точки А, В и С, такие, что АdВ и ВdС. Покажем, что точки А и С находятся в бинарном отношении d. Предположим противное, на отрезке АС существует точка Р прямой а (рис. 7). Проверим, что таких классов эквивалентности ровно два. Для этого достаточно доказать, если точки А и С и В и С не эквивалентны, то тогда точки А и В в свою очередь эквивалентны друг другу. Так как точки А и С и В и С не находятся в отношении эквивалентности d, прямая а пересекает отрезки АС и ВС точках Р и Q (см. рис. 7). Но тогда, в силу аксиомы Паша, эта прямая не может пересекать отрезок АВ. Поэтому точки А и В эквивалентны друг другу. Теорема доказана. Каждый из классов эквивалентностей, определенных в теореме 3.2, носит название полуплоскости. Таким образом, любая прямая плоскости разбивает ее на две полуплоскости, для которых она служит границей. Аналогично понятию полуплоскости вводится понятие полупространства. Доказывается теорема, в которой утверждается, что любая плоскость a пространства разбивает точки пространства на два множества. Отрезок, концы которого составляют точки одного множества, не имеет с плоскостью a общих точек. Если же концы отрезка принадлежат различным множествам, то такой отрезок имеет в качестве внутренней точку плоскости a. Доказательство этого утверждения аналогично доказательству теоремы 3.2, мы его приводить не будем. Определим понятие внутренней точки угла. Пусть дан угол Справедливы следующие утверждения. 10. Если луч с началом в вершине угла содержит хотя бы одну его внутреннюю точку, то он является внутренним лучом этого угла. 20. Если концы отрезка расположены на двух различных сторонах угла, то любая внутренняя точка отрезка является внутренней точкой угла. 30. Любой внутренний луч угла пересекает отрезок, концы которого находятся на сторонах угла.. Мы рассмотрим доказательства этих утверждений позже, в параграфе 5. C помощью аксиом второй группы определяются понятия ломанной линии, треугольника, многоугольника, понятие внутренней области простого многоугольника и доказывается, что простой многоугольник разбивает плоскость на две области, внутреннюю и внешнюю по отношению к нему. Третью группу аксиом Гильберта трехмерного евклидова пространства составляют так называемые аксиомы конгруэнтности. Пусть S – множество отрезков, А – множество углов. На декартовых произведениях Заметим, что введенное таким образом отношение не является отношением основных объектов рассматриваемой аксиоматики, т.е. точек прямых и плоскостей. Ввести третью группу аксиом можно только тогда, когда определены понятия отрезка и угла, т.е. введены первая и вторая группы аксиом Гильберта. Условимся также называть конгруэнтные отрезки или углы также геометрически равными или просто равными отрезками или углами, термин «конгруэнтные», в том случае, когда это не приводит к недоразумениям, будем заменять термином «равные» и обозначать символом «=».
|

 , где М – множество точек, введем 3 -местное отношение d. Если упорядоченная тройка точек (А, В, С) принадлежит этому отношению, то будем говорить, что точка В лежит между точками А и С и использовать при этом обозначение: А-В-С. Введенное отношение должно удовлетворять следующим аксиомам:
, где М – множество точек, введем 3 -местное отношение d. Если упорядоченная тройка точек (А, В, С) принадлежит этому отношению, то будем говорить, что точка В лежит между точками А и С и использовать при этом обозначение: А-В-С. Введенное отношение должно удовлетворять следующим аксиомам: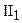 . Если точка В лежит между точками А и С, то А, В, С – три различные точки одной прямой, и при этом В лежит между С и А.
. Если точка В лежит между точками А и С, то А, В, С – три различные точки одной прямой, и при этом В лежит между С и А.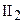 . Какова бы ни были точки А и В, существует по крайней мере одна точка С, такая, что В лежит между А и С.
. Какова бы ни были точки А и В, существует по крайней мере одна точка С, такая, что В лежит между А и С.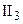 . Среди любых трех точек прямой существует не более одной, лежащей между двумя другими.
. Среди любых трех точек прямой существует не более одной, лежащей между двумя другими.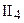 . (Аксиома Паша) Пусть А, В и С – три точки, не лежащие на одной прямой, а l – прямая плоскости АВС, на проходящая через эти точки. Тогда, если прямая l проходит через точку отрезка АВ, то она содержит либо точку отрезка АС, либо точку отрезка ВС.
. (Аксиома Паша) Пусть А, В и С – три точки, не лежащие на одной прямой, а l – прямая плоскости АВС, на проходящая через эти точки. Тогда, если прямая l проходит через точку отрезка АВ, то она содержит либо точку отрезка АС, либо точку отрезка ВС. . Рассмотрим важнейшее понятие элементарной геометрии – понятие полуплоскости.
. Рассмотрим важнейшее понятие элементарной геометрии – понятие полуплоскости. тать, что любая точка находится в бинарном отношении d сама с собой. Покажем, что для любой точки А, не принадлежащей прямой а, существуют точки, отличные от А, как находящиеся, так и не находящиеся с ней в бинарном отношении. Выберем произвольную точку Р прямой а (см. рис.6). Тогда в соответствии с аксиомой
тать, что любая точка находится в бинарном отношении d сама с собой. Покажем, что для любой точки А, не принадлежащей прямой а, существуют точки, отличные от А, как находящиеся, так и не находящиеся с ней в бинарном отношении. Выберем произвольную точку Р прямой а (см. рис.6). Тогда в соответствии с аксиомой 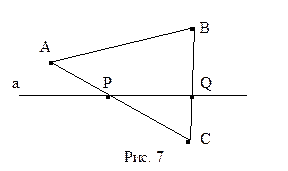 Тогда в силу аксиомы
Тогда в силу аксиомы  . Рассмотрим прямую ОА, содержащую луч ОА, сторону этого угла. Ясно, что точки луча ОВ принадлежит одной полуплоскости a относительно прямой ОА. Аналогично, точки луча ОА, стороны данного угла, принадлежат одной полуплоскости b, границу которой составляет
. Рассмотрим прямую ОА, содержащую луч ОА, сторону этого угла. Ясно, что точки луча ОВ принадлежит одной полуплоскости a относительно прямой ОА. Аналогично, точки луча ОА, стороны данного угла, принадлежат одной полуплоскости b, границу которой составляет 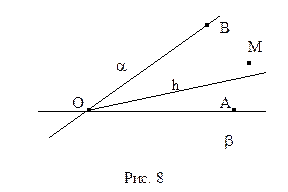 прямая ОВ (рис. 8). Точки, принадлежащие пересечению полуплоскостей a и b, называются внутренними точками угла. На рисунке 8 точка М – внутренняя точка
прямая ОВ (рис. 8). Точки, принадлежащие пересечению полуплоскостей a и b, называются внутренними точками угла. На рисунке 8 точка М – внутренняя точка 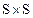 и
и  введем бинарные отношения, которые будем называть отношением конгруэнтности.
введем бинарные отношения, которые будем называть отношением конгруэнтности.


