Аксиомы непрерывности.
Четвертая группа состоит из двух аксиом.
Условимся обозначать через отрезок [AB] множество, состоящее из точек А и В и всех внутренних точек отрезка АВ. Можно доказать, что при выполнении аксиом первых трех групп аксиоматики Гильберта, аксиомы Теорема 4.3. Пусть дано разбиение точек отрезка [AB] на два класса (множества) 1. 2. 3. любая точка класса Тогда существует такая точка Доказательство этой теоремы мы не приводим. Читатель может познакомиться с ним в пособии [6]. Разбиение отрезка на классы, удовлетворяющие условию теоремы 4.3, называют дедекиндовым сечением, при этом точка Аксиомы первых четырех групп аксиоматики Гильберта позволяют доказать известные теоремы о пересечении прямых и окружностей, а также теорему о существовании перпендикуляра, опущенного из точки на окружность. С помощью этих аксиом строится теория измерения отрезков и углов, с которой мы познакомимся в последующих разделах пособия. Теория же измерения отрезков установает биектвное соответствие между множеством точек прямой и множеством действительных чисел, при котором сохраняется отношение порядка. Геометрическую теорию, построенную на аксиомах принадлежности, порядка, конгруэнтности и непрерывности, называют абсолютной геометрией. Все утверждения, доказанные ранее в параграфах 3 и 4, являются утверждениями абсолютной геометрии. Теорема 4.2 позволяет утверждать, что в абсолютной геометрии существуют непересекающиеся прямые. Для обоснования теории параллельных прямых евклидовой геометрии Д. Гильберт вводит еще одну группу аксиом.
|

 (Аксиома Архимеда). Пусть даны два отрезка АВ и CD. Тогда на прямой АВ существует такая конечная система, состоящая из n точек
(Аксиома Архимеда). Пусть даны два отрезка АВ и CD. Тогда на прямой АВ существует такая конечная система, состоящая из n точек 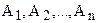 , расположенных так, что точка
, расположенных так, что точка 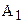 лежит между точками А и
лежит между точками А и  , точка
, точка  и так далее. При этом отрезки
и так далее. При этом отрезки  равны отрезку CD (рис. 12).
равны отрезку CD (рис. 12). 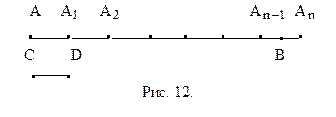 Тогда точка В лежит между
Тогда точка В лежит между  и
и  .
. (Аксиома Кантора) Пусть на произвольной прямой а дана бесконечная система отрезков
(Аксиома Кантора) Пусть на произвольной прямой а дана бесконечная система отрезков  ,
,  ,…,
,…,  …, из которых каждый последующий лежит внутри предыдущего. Пусть далее, для любого отрезка CD найдется такой номер n, что
…, из которых каждый последующий лежит внутри предыдущего. Пусть далее, для любого отрезка CD найдется такой номер n, что  . Тогда на прямой а существует такая точка Х, которая лежит внутри отрезков
. Тогда на прямой а существует такая точка Х, которая лежит внутри отрезков  Легко видеть, что аксиома
Легко видеть, что аксиома  для любого номера nпротиворечит аксиоме
для любого номера nпротиворечит аксиоме  и
и  , удовлетворяющих условиям:
, удовлетворяющих условиям: Æ;
Æ; и классы
и классы  отрезка [AB], для которой любая точка, лежащая между А и
отрезка [AB], для которой любая точка, лежащая между А и 


