Определение внутренней нормы доходности инвестиционных проектов.
Внутренняя норма доходности, прибыли (international rate of return -IRR) является показателем, широко используемым при анализе эффективности инвестиционных проектов. Реализация любого инвестиционного проекта требует привлечения финансовых ресурсов, за которые всегда необходимо платить. Так, за заемные средства платят проценты, за привлеченный акционерный капитал — дивиденды и т.д. Показатель, характеризующий относительный уровень этих расходов, является ценой за использованный (авансируемый) капитал (СС). При финансировании проекта из различных источников этот показатель определяется по формуле средней арифметической взвешенной. Чтобы обеспечить доход от инвестированных средств или, по крайней мере, их окупаемость, необходимо добиться такого положения, когда чистая текущая стоимость будет больше нуля или равна ему. Для этого необходимо подобрать такую процентную ставку для дисконтирования членов потока платежей, которая обеспечит получение выражений NPV > 0 или NPV = 0. Такая ставка (барьерный коэффициент) должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке с учетом фактора риска. Чем больше внутренняя норма прибыли превышает принятый инвестором (фирмой) барьерный коэффициент, тем больше запас прочности проекта и тем меньше риск ошибки при оценке величин будущих денежных поступлений. Внутренняя норма доходности (ВНД, IRR) представляет собой ту норму дисконта, при которой дисконтированные притоки денежных средств по проекту равны дисконтированным оттокам. Т.е. коэффициент, при котором дисконтированная стоимость чистых поступлений от инвестиционного проекта равна дисконтированной стоимости инвестиций, а величина чистого дисконтированного дохода – нулю, т.е. при начислении на сумму инвестиций процентов по ставке, равной внутренней норме доходности, обеспечивается получение распределенного во времени дохода. Для расчета ВНД используют те же приемы и формулы, что и для чистого приведенного дохода. Основная формула для ее расчета имеет вид:
Ее вычисление осуществляется на компьютере со специальной программой. (За исключением случая, когда срок реализации проекта не превышает 2-х лет; в этом случае ее решение сводится к решению обычного квадратного уравнения). Пример 12. Рассчитать внутреннюю норму доходности для проекта со следующими условиями: величина инвестиций – 500 тыс. грн., а денежные поступления по годам составляют: в первый год – 300 тыс. грн., во второй – 1400 тыс. грн. Решим задачу, используя формулу 4.12. Имеем:
заменим (1+ ВНД) на Х, следовательно:
– 500 Х 2 + 300 Х + 1400 = 0; Х1,2 = Х = 2, значит ВНД = 1 или 100% В обычных условиях ВНД определяют так называемым итеративным способом. Показатель внутренней нормы доходности характеризует максимально допустимый относительный уровень расходов, которые могут быть произведены при реализации данного проекта. Например, если для реализации проекта получена банковская ссуда, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которой делает проект убыточным. Таким образом, смысл этого показателя заключается в том, что инвестор должен сравнить полученное для инвестиционного проекта значение IRR с ценой привлеченных финансовых ресурсов (cost of capital – СС). Если IRR > СС, то проект следует принять; IRR < СС, проект следует отвергнуть; IRR= СС- проект ни прибыльный, ни убыточный. Показатель внутренней нормы доходности может служить основой для ранжирования инвестиционных проектов по степени их выгодности, но при тождественности основных исходных параметров сравниваемых проектов: 1. Одинаковой продолжительности осуществления проектов; 2. Одинаковых уровнях риска; 3. Равной сумме инвестиций и примерно равных суммах ежегодных доходов (по годам функционирования объекта инвестиций). Следует иметь в виду, что различные ряды потока реальных денег могут создавать одинаковую внутреннюю норму прибыли. Кроме того, вероятен случай, когда предпочтение следует отдать проекту с меньшей ВНД, но все еще превышающей коэффициент окупаемости, а не проекту с более высокой ВНД, но с определенной структурой реальных денег. Методвнутренней нормы доходности рекомендуется использовать с осторожностью и при наличии двух или более исключающих друг друга проектов (взаимоисключающими являются проекты, если принятие одного из них означает отклонение другого), например, когда имеется только один строительный участок или реконструируется завод. Проблема здесь не в принятии или отклонении проекта, а в том, какую из двух осуществляемых альтернатив нужно выбрать. Считается, что если метод используется правильно, то он приведет к такому же решению, что и ЧПД. Практическое применение данного метода сводится к последовательной итерации, с помощью которой находится дисконтирующий множитель, обеспечивающий равенство NPV = 0. Ориентируясь на существующие в момент анализа процентные ставки на ссудный капитал, выбираются два значения коэффициента дисконтирования V1 < V2 таким образом, чтобы в интервале (V1, V2) функция NРV=f(V} меняла свое значение с «+» на «–» или наоборот. Далее используют формулу:
где i1 – л значение процентной ставки в дисконтном множителе, при котором f(i1) < 0;f(i2)> 0; i2 – значение процентной ставки в дисконтном множителе, при котором f (i2) < 0; f (i2) > 0. Точность вычислений обратно длине интервала (i1, i2). Поэтому наилучшая аппроксимация достигается в случае, когда длина интервала принимается минимальной (1%). Пример 13. Требуется определить значение IRR для проекта, рассчитанного на 3 года, требующего инвестиции в размере 20 млн. грн. и имеющего предполагаемые денежные поступления в размере P1 = 6 млн. грн. (первый год), P2 = 8 млн. грн. (второй год) и P3 = 14 млн. грн. (третий год). Возьмем два произвольных значения процентной ставки для коэффициента дисконтирования: i1= 15% и i2 = 20%. Соответствующие расчеты приведены в табл.
По данным расчета I и II вычислим значение IRR. 1)
Уточним величину ставки, для чего примем значения процентных ставок, равное i1 = 16%; i2 = 17%. Произведем новый расчет.
IRR = 16,23% является верхним пределом процентной ставки, по которой фирма может окупить кредит для финансирования инвестиционного проекта. Для получения прибыли фирма должна брать кредит по ставке менее 16,23%. Расчет индекса рентабельности и коэффициента эффективности инвестиций. Метод расчета индекса рентабельности (profitability index-PI) является как бы продолжением метода расчета чистого приведенного дохода – NPV. Показатель РI в отличие от показателя NPV является относительной величиной. Благодаря этому он очень удобен при выборе одного проекта из ряда альтернативных, имеющих примерно одинаковые значения NPV, либо при комплектовании портфеля инвестиций с максимальным суммарным значением NPV. Если инвестиции осуществлены разовым вложением, то данный показатель рассчитывается по формуле:
где Рk — чистый доход; IС— стартовые инвестиции Vt — дисконтный множитель. Если инвестиции представляют собой некоторый поток, то
Если показатель РI=1, то это означает, что доходность инвестиций точно соответствует нормативу рентабельности (ставке сравнения). При РI<1 инвестиции нерентабельны, так как не обеспечивают этот норматив.
|

 (8.12.)
(8.12.)
 ;
; ;
; , (8.13.)
, (8.13.) i1 =15%
i1 =15%
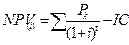
 I2=20%
I2=20%
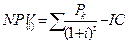




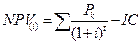
 2)
2) 
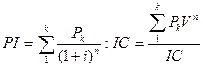 , (8.14.)
, (8.14.) , (8.15.)
, (8.15.) где IС – размеры инвестиционных затрат в периоды t = 1, 2,...,n..
где IС – размеры инвестиционных затрат в периоды t = 1, 2,...,n.. Пример 13. Показатели современных величин вложений равны 5,1568 млн. грн., а современная величина чистых доходов составляет 5,4452 млн. грн. При этих условиях индекс рентабельности будет равен:
Пример 13. Показатели современных величин вложений равны 5,1568 млн. грн., а современная величина чистых доходов составляет 5,4452 млн. грн. При этих условиях индекс рентабельности будет равен: .
.


