Методы нахождения ранга.
Метод целенаправленного перебора миноров. Если все миноры первого порядка (элементы матрицы) равны нулю, то r =0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны 0, то r =1. Если хотя бы один минор второго порядка отличен от 0, то исследуют миноры третьего порядка. Если они все равны 0, то r = 2. В противном случае (если хотя бы один минор третьего порядка, не равный 0) исследуют миноры 4-го порядка. Так поступают до тех пор, пока не обнаружится одно из двух: либо все миноры (К+1)-го порядка равны 0 МК+1=0, либо миноры порядка (К+1)-го не существует, тогда ранг равен К: r = K. если пользоваться только определением, то требуется вычисление большого количества определителей, поэтому этот метод неэффективен при больших m, n. Пример. Найти ранг матрицы А= Решение. Так как среди миноров первого порядка элементов матрицы есть не равные 0, то r (A)≥1. Проверим, может ли быть ранг равен двум. Для этого найдем хотя бы один минор второго порядка, не равный 0. Например, Теперь вычислим все миноры третьего порядка. Но таких только один- это определитель данной матрицы. Он равен 0: Значит, ранг матрицы равен двум: r (A)=2. Метод окаймляющих миноров. Определ. Минор МК+1 порядка К+1, содержащий в себе минор МК порядка К, называется окаймляющим минором МК. Пример. Для матрицы А=
Если у матрицы А существует минор МК≠0, а все окаймляющие его миноры МК+1=0, то ранг r (A) = K/ Метод элементарных преобразований Гаусса. Пример. Привести к трапециевидной форме матрицу и найти ее ранг: А= Решение. Умножая первую строку последовательно на -2, -4, -5 и прибавляя соответственно ко второй, третьей и четвертой строкам, получим новую матрицу, эквивалентную данной:
Умножили вторую строку на (-1) и сложив сначала с третьей строкой, а затем с четвертой строкой, получили эквивалентную матрицу
|



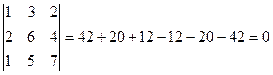 .
. минором третьего порядка М3, окаймляющим минор второго порядка М2=
минором третьего порядка М3, окаймляющим минор второго порядка М2= 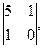 является М3=
является М3=  или М3 =
или М3 =  окаймляющий минор М3 не единственный.
окаймляющий минор М3 не единственный.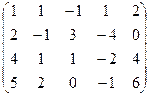

 . Полученная трапециевидная матрица имеет две ненулевых строки, значит, ее ранг равен двум, как и ранг эквивалентной ей матрицы А: r (A) =2.
. Полученная трапециевидная матрица имеет две ненулевых строки, значит, ее ранг равен двум, как и ранг эквивалентной ей матрицы А: r (A) =2.


