Раздел 2. Выбор в условиях неопределенности
1. Рассмотрите индивида, которому предложили выбрать между получением 7 д.е. и участием в лотерее, позволяющей выиграть 20 д.е. с вероятностью (а) Если известно, что индивид – рискофоб, то что он выберет? (б) Если известно, что индивид – рискофил, то что он выберет? (в) Если известно, что индивид нейтрален к риску, то что он выберет? (г) Предположим теперь, что элементарная функция полезности индивида имеет вид: 2. Пусть лотерея L обещает выплату в размере 3. Г-жа A рассматривает альтернативы проведения субботнего вечера. Она может пойти в ресторан “Ocean View”. Такое времяпрепровождение она оценивает в 49 д.ед. Кроме того, г-жа А может пойти в ресторан “Renaissance”. Если в “Renaissance” будет выступать “Flabrum euri”, то такой вечер оценивается г-жой А в 100 д.ед. Если же концерта не будет, то оценка такого вечера 16 д.ед. Обычно по субботам в ресторане “ Renaissance” действительно выступает “Flabrum euri”, и вероятность такого события г-жа А оценивает в 75 %. Она может позвонить в справочную службу ресторана, чтобы узнать будет концерт или нет. За неуплату у А отключили стационарный телефон. Поэтому она может сделать звонок только с мобильного телефона. В соответствии с ее тарифом для нее звонок платный. Предпочтения А описываются функцией ожидаемой полезности с элементарной функцией полезности (а) Какова максимальная цена за звонок, которую согласится заплатить А? (б) Приведите иллюстрации в пространстве «богатство-полезность» и пространстве контингентных благ. 4. Рассмотрите следующие элементарные функции полезности: (1) (3) (5) (7) (а) Какая/какие из указанных функций полезности описывают предпочтения индивида, обладающего положительным богатством, если
(б) Есть ли среди указанных функций полезности такие, что индивид при одном уровне богатства является рискофобом, а при другом - рискофилом? 5. Состояние г-на Х оценивается в 64 д.е., однако часть этого богатства, равная 28 д.е., хранится на депозите в банке Y. По мнению экспертов банк Y находится на грани банкротства, в связи с чем вероятность потери вложенных в банк средств оценивается в 25%. Будем считать, что предпочтения г-на Х описываются функцией ожидаемой полезности с элементарной функцией полезности (а) Фирма Z, скупающая проблемные долги, предложила господину Х продать его депозит в банке Y за 13 д.е. Пойдет ли г-н Х на такую сделку? Изменится ли ваш ответ, если г-ну Х предложат 26 д.е.? (б) Проиллюстрируйте ваш ответ на пункт (а) в пространстве контингентных благ: (1) определите контингентные блага; (2) изобразите кривые безразличия г-на Х и укажите их наклон; (3) отметьте на рисунке точки, соответствующие случаям, когда г-н Х продает свой актив и отказывается от сделки. 6. Две подруги Анна и Мария, предпочтения которых могут быть описаны элементарными функциями полезности вида (а) Будет ли Анна инвестировать средства в проект? Будет ли Мария инвестировать средства в проект? Проиллюстрируйте решение графически в пространстве контингентных благ и в пространстве богатство-полезность. (б) Предположим, что проекты независимы, и у подруг есть возможность либо объединить свои риски, либо участвовать в индивидуальном инвестиционном проекте. При объединении рисков полученные от инвестиций средства (как выигрыши, так и потери) подруги будут делить пополам, т.е., состояние обеих подруг будет одинаковым. Согласится ли каждая из подруг принять подобные условия и участвовать в проектах, объединив свои богатства? (в) Какую максимальную сумму будет готова заплатить Мария Анне за то, чтобы подруги участвовали в рисковых проектах совместно? Если Мария заплатит Анне указанную сумму, изменит ли Анна свое решение относительно совместного участия в проектах? (г) Предположим, что до принятия решения о вложении средств в индивидуальный рисковый проект, каждая из подруг имеет возможность получить информацию о том, будут ли инвестиции успешны или нет, заплатив за эту информацию некоторую сумму денег. Найдите максимальную сумму денег, которую каждая из подруг захочет заплатить за информацию. Проиллюстрируйте решение графически в пространстве контингентных благ. 7. Рассмотрите модель спроса на страховку для индивида – рискофоба, предпочтения которого описываются функцией ожидаемой полезности с дифференцируемой элементарной функцией полезности. Пусть цена единицы страховки 8. Рассмотрите модель спроса на страховку для индивида, обладающего богатством (а) Какое количество страховки приобретет данный индивид? (б) Как изменится ваш ответ на пункт (а), если цена единицы страховки составит (в) Опишите задачу выбора оптимальной величины страховки в терминах контингентных (обусловленных) благ.
(г) Предположим теперь, что индивид нейтрален к риску. На какую сумму застрахуется данный индивид при 9. Рассмотрите модель спроса на страховку для индивида, обладающего богатством (а) Определите состояния природы и соответствующие контингентные блага в данной модели. Выведите бюджетное ограничение в терминах контингентных благ и изобразите графически. (б) При каких значениях (в) Существуют ли значения 10. Рассмотрите индивида-рискофоба, который решает, как ему распределить свое богатство (а) Выпишите задачу максимизации ожидаемой полезности индивида и условия первого порядка. В пунктах (б)-(в) считайте, что индивид предъявляет положительный спрос на оба актива. (б) Как изменится спрос на безрисковый актив при малом увеличении параметра (в) Как изменится спрос на рисковый актив при малом увеличении вероятности (г) Опишите задачу выбора оптимального портфеля в терминах контингентных (обусловленных) благ:
(д) Предположим теперь, что индивид нейтрален к риску. Найдите оптимальную величину вложений в рисковый и безрисковый активы. Приведите графическую иллюстрацию. 11. Вы располагаете богатством 500 д.е. Ваш приятель хочет открыть свой магазин и просит у Вас вложить в его бизнес некоторую сумму денег. В замен он обещает, что Вы станете совладельцем. Тогда, если торговля будет успешной, то с каждого вложенного Вами рубля Вы получите 4 д.е. Но если магазин прогорит, то Вы потеряете свои деньги. Изучая статистику Вы поняли, что вероятность успеха равна 2/5. Ваша элементарная функция полезности имеет вид: (а) Предположим, Ваш приятель просит у Вас вложить в магазин 200 д.е. Согласитесь ли Вы с предложением приятеля? (б) Выпишите условие, характеризующее максимальную сумму денег, которую Вы готовы вложить в магазин. (в) Предположим, что Ваш приятель просит у Вас не определенную сумму, а предлагает Вам самому решить, сколько вложить, чтобы стать совладельцем. Какую сумму Вы дадите? (г) Определите состояния природы и соответствующие контингентные блага в данной модели. (д) Выведите бюджетное ограничение в терминах контингентных благ и изобразите графически. (е) Изобразите на графике Ваш оптимальный выбор. (ж) Предположим теперь, что Вы нейтральны к риску. Каков будет Ваш оптимальный выбор в этом случае? Приведите графическую иллюстрацию. 12. Рассмотрите налогоплательщика, имеющего доход равный Считайте, что налогоплательщик – рискофоб, имеющий предпочтения, не зависящие от состояния, и представимые функцией ожидаемой полезности. (а) Определите состояния природы и соответствующие контингентные блага в данной модели. (б) Выпишите задачу налогоплательщика, из которой определяется оптимальная величина декларируемого дохода и условия, характеризующие внутреннее решение. (в) Покажите, что условие Далее считайте, что условие, приведенное в п. (в) выполнено. (г) Как изменится величина недекларируемого дохода при малом увеличении штрафа (д) Выведите бюджетное ограничение в терминах теории контингентных благ и изобразите графически. (е) Приведите графическую иллюстрацию условия, приведенного в п. (в), изобразив на одном рисунке бюджетное ограничение и кривые безразличия индивида. (ж) Предположим теперь, что налогоплательщик нейтрален к риску. Будет ли он уклоняться от уплаты налогов? Изобразите решение графически. 13. * Рассмотрите экономику обмена с одним физическим благом, двумя потребителями (А и В) и двумя состояниями мира (1 и 2). Пусть первоначальные запасы потребителей описываются векторами (а) Покажите, что во всех внутренних Парето-оптимальных распределениях уровень потребления каждого потребителя будет выше в том состоянии мира, которое он считает более вероятным. (б) Будет ли верен результат пункта (а), если потребитель А нейтрален к риску? 14. * Рассмотрите экономику обмена с одним физическим благом, двумя потребителями (А и В) и двумя состояниями мира (1 и 2). Пусть первоначальные запасы потребителей описываются векторами (а) Покажите, что во всех внутренних Парето-оптимальных распределениях потребители будут полностью застрахованы от риска (т.е. (б) Приведите альтернативное доказательство утверждения из пункта (а): покажите, что для любого допустимого внутреннего распределения такого, что (в) Покажите, что во внутреннем равновесии Эрроу-Дебре равновесное отношение цен равно отношению вероятностей наступления соответствующих состояний мира. (г) Предположим теперь, что потребитель А нейтрален к риску, а все остальные условия задачи остаются неизменными. Будет ли потребитель В по-прежнему полностью застрахован от риска в любом внутреннем Парето-оптимальном распределении? 15. * Рассмотрите экономику обмена с одним физическим благом, двумя состояниями мира (1 и 2) и тремя потребителями (A, B и С). Запасы физического блага у потребителей в состояниях мира 1 и 2, соответственно, составляют Раздел 3. Теория поведения производителя (фирмы) 1. Пусть фирма занимается производством столов из ножек и столешниц. Если для производства одного стола требуется одна столешница и четыре ножки, то какой вид имеет производственная функция данной фирмы? Изобразите изокванты. 2. Пусть производственная функция имеет вид 3. Пусть технология фирмы описывается производственной функцией Кобба-Дугласа вида (а) Выпишите задачу фирмы в краткосрочном периоде, считая первый фактор фиксированным. Найдите спрос на первый фактор и предложение фирмы. (б) Выпишите задачу максимизации прибыли и условия, характеризующее ее решение. Найдите функции спроса на факторы производства и функцию предложения фирмы. (в) Покажите, что в пункте (б) доля расходов на каждый фактор производства постоянна. (г) Воспользовавшись результатом пункта (б), объясните, что происходит с функцией предложения в случае (д) Что можно сказать о решении задачи максимизации прибыли в случае 4. Рассмотрите фирму, которая производит готовую продукцию, используя два фактора производства, согласно производственной функции 5. Рассмотрите фирму, которая производит готовую продукцию, используя два фактора производства, согласно производственной функции (а) Верно ли, что производственная функция (б) Изобразите изокванту, соответствующую уровню выпуска (в) Пусть цена готовой продукции равна 6. Пусть технология фирмы описывается производственной функцией (а) Выпишите задачу максимизации прибыли и условия, характеризующие ее решение. Приведите графическую иллюстрацию. (б) Предположим, правительство ввело потоварный налог 7. Рассмотрите фирму, которая производит готовую продукцию, используя два фактора производства, труд и капитал согласно производственной функции 8. Пусть при ценах 9. Докажите не пользуясь дифференцированием, что выручка максимизирующей прибыль фирмы не возрастет при пропорциональном увеличении цен всех факторов производства. 10. Рассмотрите фирму, которая производит готовую продукцию, используя единственный фактор производства. При цене выпуска
11. Пусть производственная функция фирмы имеет вид (i) (ii) (iii) (а) Вычислите минимальные издержки производства выпуска (б) Найдите функции условного спроса на факторы производства, и функцию издержек фирмы. 12. Верно ли,что если технология характеризуется постоянной отдачей от масштаба, то функция издержек линейна по выпуску? Что можно сказать в этом случае о средних издержках? 13. Пусть при ценах 14. Пусть фирма владеет двумя заводами по производству некоторого товара. На первом заводе продукция производится в соответствии с функцией издержек 15. Рассмотрите фирму, минимизирующую издержки, которая производит готовую продукцию с помощью двух факторов производства (труда и капитала). Предположим, что заработная плата, возросла, и фирма на это отреагировала изменением спроса на факторы производства, но сохранила выпуск постоянным. Что произойдет с объемом труда, используемым фирмой? 16. Пусть функция издержек фирмы в долгосрочном периоде (при фиксированных ценах факторов производства) имеет вид: (а) Найдите средние и предельные издержки фирмы и приведите графическую иллюстрацию. (б) Найдите функцию предложения фирмы и приведите графическую иллюстрацию.
|

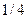 и 4 д.е. с вероятностью
и 4 д.е. с вероятностью 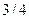 .
. . Каково отношению к риску у данного индивида? Что выберет данный индивид? Как изменится ваш ответ, если индивиду предлагается выбор между данной лотереей и гарантированным получением 4,5 д.е.?
. Каково отношению к риску у данного индивида? Что выберет данный индивид? Как изменится ваш ответ, если индивиду предлагается выбор между данной лотереей и гарантированным получением 4,5 д.е.?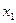 с вероятностью
с вероятностью 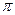 и в размере
и в размере 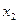 в противном случае. Рассмотрите нейтрального к риску индивида, обладающего богатством
в противном случае. Рассмотрите нейтрального к риску индивида, обладающего богатством  . Обозначим через
. Обозначим через 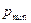 - минимальную цену, по которой индивид согласится продать данную лотерею, если он ею владеет, а через
- минимальную цену, по которой индивид согласится продать данную лотерею, если он ею владеет, а через 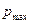 - максимальную цену, за которую он согласится купить данную лотерею, если он ею не владеет. Чему равны
- максимальную цену, за которую он согласится купить данную лотерею, если он ею не владеет. Чему равны 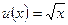 .
.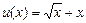 ; (2)
; (2) 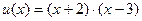 ;
;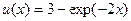 ; (4)
; (4)  ;
;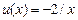 ; (6)
; (6) 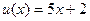 ;
;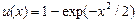 ; (8)
; (8) 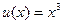 .
.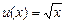 .
.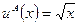 и
и 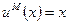 , где
, где  богатство в тыс. долларов, собираются вложить деньги в инвестиционные проекты, вероятность успеха в которых оценивается, как ¼. Если деньги будут вложены удачно в инвестиционный проект, предлагаемый Анне, то ее состояние составит 256 тыс. долларов, если нет, то ее состояние составит только 36 тыс. долларов. Если деньги будут вложены удачно в инвестиционный проект, предлагаемый Марии, то ее состояние составит 100 тыс. долларов, если нет, то ее состояние составит только 52 тыс. долларов. В настоящее время состояние каждой из подруг оценивается в 64 тыс. долларов.
богатство в тыс. долларов, собираются вложить деньги в инвестиционные проекты, вероятность успеха в которых оценивается, как ¼. Если деньги будут вложены удачно в инвестиционный проект, предлагаемый Анне, то ее состояние составит 256 тыс. долларов, если нет, то ее состояние составит только 36 тыс. долларов. Если деньги будут вложены удачно в инвестиционный проект, предлагаемый Марии, то ее состояние составит 100 тыс. долларов, если нет, то ее состояние составит только 52 тыс. долларов. В настоящее время состояние каждой из подруг оценивается в 64 тыс. долларов.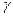 превышает вероятность наступления страхового случая
превышает вероятность наступления страхового случая 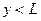 . Приведите графическую иллюстрацию в пространстве контингентных благ.
. Приведите графическую иллюстрацию в пространстве контингентных благ.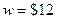 тыс. Предположим, с вероятностью
тыс. Предположим, с вероятностью 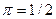 может произойти несчастный случай, в результате которого индивид потеряет часть этого богатства, а именно,
может произойти несчастный случай, в результате которого индивид потеряет часть этого богатства, а именно,  тыс. Индивид имеет возможность приобрести страховку по цене
тыс. Индивид имеет возможность приобрести страховку по цене 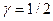 за единицу страхового покрытия. Предпочтения индивида описываются функцией ожидаемой полезности с элементарной функцией полезности
за единицу страхового покрытия. Предпочтения индивида описываются функцией ожидаемой полезности с элементарной функцией полезности 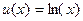 .
.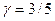 ?
?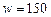 д.е. Предположим, с вероятностью
д.е. Предположим, с вероятностью 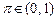 может произойти несчастный случай, в результате которого индивид потеряет часть этого богатства, а именно
может произойти несчастный случай, в результате которого индивид потеряет часть этого богатства, а именно  д.е. Индивид имеет возможность приобрести страховку по цене
д.е. Индивид имеет возможность приобрести страховку по цене 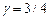 за единицу страхового покрытия у нейтральной к риску страховой компании, не имеющей операционных издержек, причем страхование на сумму, превышающую потери, запрещено. Элементарная функция полезности индивида имеет вид
за единицу страхового покрытия у нейтральной к риску страховой компании, не имеющей операционных издержек, причем страхование на сумму, превышающую потери, запрещено. Элементарная функция полезности индивида имеет вид 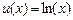 .
.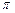 индивид страхуется полностью? Приведите иллюстрацию в пространстве контингентных благ.
индивид страхуется полностью? Приведите иллюстрацию в пространстве контингентных благ. с вероятностью
с вероятностью  , и
, и 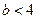 в противном случае, причем
в противном случае, причем 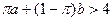 . Пусть предпочтения индивида представимы функцией ожидаемой полезности с дифференцируемой элементарной функцией полезности.
. Пусть предпочтения индивида представимы функцией ожидаемой полезности с дифференцируемой элементарной функцией полезности.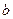 ? Проинтерпретируйте полученный результат.
? Проинтерпретируйте полученный результат.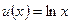 .
. , который должен подать декларацию о доходах в налоговую инспекцию. Обозначим через
, который должен подать декларацию о доходах в налоговую инспекцию. Обозначим через 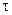 ставку подоходного налога (
ставку подоходного налога (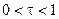 ). Налогоплательщик может указать в налоговой декларации сумму, меньшую его фактического дохода, но не может указать сумму, превышающую его фактический доход. Если налоговая инспекция проведет проверку и выявит уклонение от налогов, то налогоплательщик будет вынужден не только выплатить налоги на незадекларированный доход (обозначим его через
). Налогоплательщик может указать в налоговой декларации сумму, меньшую его фактического дохода, но не может указать сумму, превышающую его фактический доход. Если налоговая инспекция проведет проверку и выявит уклонение от налогов, то налогоплательщик будет вынужден не только выплатить налоги на незадекларированный доход (обозначим его через  с каждого доллара незадекларированного дохода, причем
с каждого доллара незадекларированного дохода, причем  . Пусть вероятность проведения проверки поданной декларации равна
. Пусть вероятность проведения проверки поданной декларации равна 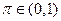 , и если она проводится, то гарантировано выявляется фактический доход налогоплательщика.
, и если она проводится, то гарантировано выявляется фактический доход налогоплательщика.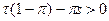 является необходимым и достаточным условием того, что налогоплательщик будет занижать свой фактический доход в налоговой декларации.
является необходимым и достаточным условием того, что налогоплательщик будет занижать свой фактический доход в налоговой декларации. ,
, 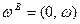 , где
, где 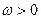 . Пусть потребитель А считает первое состояние мира более вероятным, т.е.
. Пусть потребитель А считает первое состояние мира более вероятным, т.е. 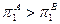 . Предположим также, что потребители являются рискофобами с предпочтениями представимыми функцией ожидаемей полезности с дифференцируемыми элементарными функциями полезности, не зависящими от состояния.
. Предположим также, что потребители являются рискофобами с предпочтениями представимыми функцией ожидаемей полезности с дифференцируемыми элементарными функциями полезности, не зависящими от состояния.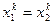 для любого потребителя
для любого потребителя 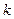 ), пользуясь дифференциальной характеристикой внутреннего Парето-оптимума.
), пользуясь дифференциальной характеристикой внутреннего Парето-оптимума.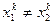 , можно построить Парето-улучшение.
, можно построить Парето-улучшение.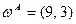 ,
,  ,
, 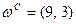 . Предпочтения всех потребителей представимы функцией ожидаемой полезности с возрастающими элементарными функциями полезности, причем элементарная функция полезности потребителя С имеет вид:
. Предпочтения всех потребителей представимы функцией ожидаемой полезности с возрастающими элементарными функциями полезности, причем элементарная функция полезности потребителя С имеет вид:  . Потребитель С считает, что первое состояние мира наступит с вероятностью
. Потребитель С считает, что первое состояние мира наступит с вероятностью 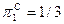 . Известно, что в равновесии Эрроу-Дебре
. Известно, что в равновесии Эрроу-Дебре  и
и  . Найдите недостающие параметры равновесия.
. Найдите недостающие параметры равновесия.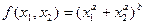 , где
, где 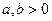 . При каких значениях параметров данная технология характеризуется убывающей, постоянной и возрастающей отдачей от масштаба?
. При каких значениях параметров данная технология характеризуется убывающей, постоянной и возрастающей отдачей от масштаба?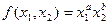 , где
, где 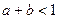 ,
, 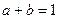 .
.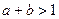 ?
?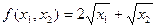 . Выпишите задачу максимизации прибыли фирмы; найдите спрос на оба фактора производства и предложение готовой продукции.
. Выпишите задачу максимизации прибыли фирмы; найдите спрос на оба фактора производства и предложение готовой продукции.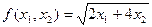 .
. описывает ту же технологию?
описывает ту же технологию?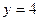 .
.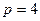 , а цены факторов составляют
, а цены факторов составляют 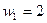 и
и 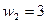 . Выпишите задачу максимизации прибыли фирмы; найдите спрос на оба фактора производства и предложение готовой продукции.
. Выпишите задачу максимизации прибыли фирмы; найдите спрос на оба фактора производства и предложение готовой продукции.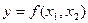 . Будем считать, что производственная функция фирмы характеризуются убывающим предельным продуктом каждого фактора. Пусть в краткосрочном периоде второй фактор фиксирован.
. Будем считать, что производственная функция фирмы характеризуются убывающим предельным продуктом каждого фактора. Пусть в краткосрочном периоде второй фактор фиксирован.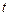 на каждую единицу первого фактора, используемую фирмой. Как изменится объем использования первого фактора, предложение готовой продукции и прибыль фирмы в результате введения налога? Приведите графическую иллюстрацию.
на каждую единицу первого фактора, используемую фирмой. Как изменится объем использования первого фактора, предложение готовой продукции и прибыль фирмы в результате введения налога? Приведите графическую иллюстрацию.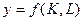 . Покажите, что спрос на труд не возрастает при увеличении ставки заработной платы. (В задаче не предполагается дифференцируемость производственной функции.)
. Покажите, что спрос на труд не возрастает при увеличении ставки заработной платы. (В задаче не предполагается дифференцируемость производственной функции.)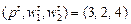 фирма выпускала 16 единиц готовой продукции, затрачивая факторы производства в количестве
фирма выпускала 16 единиц готовой продукции, затрачивая факторы производства в количестве  . Затем цены изменились, и при новых ценах
. Затем цены изменились, и при новых ценах 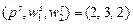 фирма произвела 13 единиц готовой продукции, затратив факторы в количестве
фирма произвела 13 единиц готовой продукции, затратив факторы в количестве 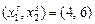 . Совместимы ли подобные наблюдения с максимизацией прибыли?
. Совместимы ли подобные наблюдения с максимизацией прибыли?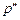 и цене фактора
и цене фактора 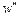 объем спроса фирмы на фактор составил
объем спроса фирмы на фактор составил 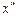 и объем выпуска составил
и объем выпуска составил 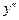 , а при ценах
, а при ценах 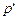 и
и 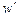 фирма выбрала
фирма выбрала 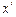 и
и  . На рисунках изображены соответствующие изопрофиты. В каком/каких из следующих случаев поведение фирмы не согласуется с максимизацией прибыли?
. На рисунках изображены соответствующие изопрофиты. В каком/каких из следующих случаев поведение фирмы не согласуется с максимизацией прибыли?
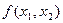 . В каждом из следующих случаев
. В каждом из следующих случаев .
.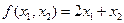 .
.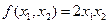 .
.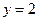 при ценах факторов
при ценах факторов 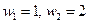 . Приведите графическую иллюстрацию.
. Приведите графическую иллюстрацию.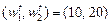 фирма использовала следующие объемы факторов производства
фирма использовала следующие объемы факторов производства 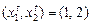 для производства 100 единиц готовой продукции. Затем цены изменились, и при новых ценах
для производства 100 единиц готовой продукции. Затем цены изменились, и при новых ценах 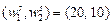 фирма производила 100 единиц готовой продукции, затратив факторы в количестве
фирма производила 100 единиц готовой продукции, затратив факторы в количестве 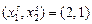 . Совместимо ли подобное поведение фирмы с минимизацией издержек?
. Совместимо ли подобное поведение фирмы с минимизацией издержек?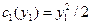 , а на втором – в соответствии с функцией издержек
, а на втором – в соответствии с функцией издержек 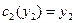 . Найдите функцию издержек фирмы.
. Найдите функцию издержек фирмы.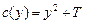 , если
, если 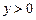 , и
, и 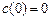 , где
, где 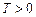 – это затраты фирмы на вход в отрасль (например, на покупку лицензии).
– это затраты фирмы на вход в отрасль (например, на покупку лицензии).


