Рентні платежі (ануїтети) та їх оцінка.
Визначення майбутньої вартості потоку платежів. Нехай інвестор протягом певного періоду часу в кінці кожного року одержує платежі, які не є однаковими. Якщо він буде інвестувати суму кожного платежу на час до закінчення даного періоду, то після його завершення одержить деяку суму грошей, яку називають майбутньою вартістю потоку платежів. Майбутню вартість потоку платежів можна визначити за формулою:
де: F - майбутня вартість потоку платежів; Сt - сума платежу за рік t; r - відсоток, під який інвестується сума Сt; n - кількість років, протягом яких проводяться виплати. Майбутня вартість звичайного ануїтету при нарахуванні складного відсотку один раз на рік. Виникають ситуації, коли отримують (або виплачують) не одну суму, а декілька. Причому виплату (отримання) цих сум проводять за такими правилами: однакова сума через рівні проміжки часу за однієї й тієї самої діючої відсоткової ставки. Такий механізм припливу (відпливу) грошей одержав назву ануїтету або ренти. Розрізняють два основних типи рент: безумовні й умовні ренти. Безумовні - ренти з фіксованим строком, тобто дати першої і останньої виплати визначені до початку ренти. Умовні ренти, в яких дата першої та останньої виплат залежить від деякої події. Рента називається звичайною (постнумерандо), якщо виплати здійснюються в кінці кожного періоду, і приведеною (авансованою, вексельною або пренумерандо), якщо виплати відбуваються на початку кожного періоду. Як і для простої величини, для ануїтету можна визначити його майбутню і теперішню вартість. Майбутню вартість ануїтету визначають як суму платежів і складних відсотків, що їх нараховують на кожній платіж на період часу, який пройшов від моменту кожного платежу до моменту останнього платежу. Визначити майбутню вартість звичайного ануїтету можна за допомогою формули:
Перетворимо формулу (23) для одержання С:
Майбутня вартість звичайного ануїтету при здійсненні виплат m разів на рік розраховується за формулою:
Майбутня вартість ануїтету при нарахуванні відсотку m разів на рік. Випадок, що розглядається, відрізняється від попереднього тим, що складний відсоток нараховується протягом року m разів, а платежі по ануїтету здійснюються тільки в кінці кожного року. Це означає, що відсотки по першому платежу нараховують з початку другого року і здійснюють m разів на рік тощо. В даному випадку майбутня вартість ануїтету дорівнює:
Приведена вартість ануїтету при нарахуванні відсотку один раз на рік. Оберненим до поняття майбутньої вартості ануїтету є поняття теперішньої вартості ануїтету – теперішня, поточна або сьогоднішня вартість майбутніх рівномірних платежів, які здійснюють через рівні проміжки часу. Вона розраховується за формулою:
де: Р – приведена вартість ануїтету. Формула приведеної вартості ануїтету може також використовуватися в тому випадку, коли позичальник бере кредит на умовах його погашення в майбутньому щорічними рівними платежами. Для цього з формули (3.32) виражають величину С:
де: Р – сума кредиту; r – відсоток по кредиту; С – платіж по кредиту; N – термін дії кредиту. Приведена вартість ануїтету при здійсненні виплат m разів на рік. Для випадку, що розглядається, приведену вартість ануїтету знаходять за допомогою наступної формули:
Приведена вартість ануїтету при нарахуванні відсотку m разів на рік розраховується за формулою:
Довічна рента. Довічна рента, виплати якої не обмежені ніякими строками. Майбутню вартість такого ануїтету визначити неможливо, так як вона не є кінцевою величиною. Однак можна розрахувати приведену вартість довічної ренти, скориставшись формулою (30). Оскільки для такого ануїтету n → ∞, то формула розрахунку приведеної вартості набуває вигляду:
Прикладом довічного ануїтету є безстрокові облігації та привілейовані акції, що генерують доход невизначено тривалий час, тому їх поточна теоретична вартість визначається за формулою (3.36). Найбільш простим варіантом оцінки привілейованої акції є відношення величини дивіденду до ринкової норми прибутку за акціями даного класу ризику. Доходність фінансових операцій. На фінансовому ринку інвестора цікавить результат його операцій. Результативність інвестицій порівнюють за допомогою такого показника, як доходність. Доходність – це відносний показник, що показує, який відсоток приносить 1 гривня інвестованих коштів за певний період. Доходність за період. Доходність за період - це доходність, яку інвестор одержить за певний період часу. Вона визначається за формулою:
де: r - доходність за період; Р - початкове інвестовані кошти; Рn сума, одержана через n років.
Доходність з розрахунку на рік. На фінансовому ринку виникає необхідність порівнювати доходності різних фінансових інструментів. Тому показником доходності, що зустрічається найчастіше, є доходність в розрахунку на рік. Він визначається як середнє геометричне, а саме:
де: r - доходність в розрахунку на рік; n - число років. Розрахунок доходності при нарахуванні відсотків m разів за рік:
Якщо відсоток нараховується безперервно, то доходність в розрахунку на рік можна визначити за формулою:
де: rn - доходність, виражена як відсоток, що нараховується безперервно. Для короткострокових операцій доходність визначається на підставі формул:
Для короткострокових цінних паперів також можна розрахувати ефективну доходність, тобто ефективний відсоток. Для цього можна скористатися наступною формулою (для прикладу візьмемо фінансовий рік, що дорівнює 360 дням).
де: rеф - ефективна доходність в розрахунку на рік; t - період фінансової операції (час з моменту купівлі до продажу або погашення цінного паперу); r - простий відсоток в розрахунку на рік; г, - доходність за період t.
Відсоткові ставки та інфляція. Розрізняють номінальні і реальні відсоткові ставки. Якщо темп інфляції перевищує ставку відсотку, яку одержує вкладник на вкладені кошти, то результат від фінансової операції виявиться негативним, тобто за абсолютною величиною його кошти збільшаться, а їх сукупна купівельна спроможність зменшиться. Номінальна відсоткова ставка - це відсоткова ставка без врахування інфляції. В якості номінальних виступають відсоткові ставки банківських установ. Номінальна ставка свідчить про абсолютне зростання грошових коштів інвестора. Реальна відсоткова ставка - це ставка, що скоригована на відсоток інфляції. Реальна ставка свідчить про приріст купівельної спроможності коштів інвестора. Взаємозв'язок між номінальною і реальною відсотковими ставками можна представити наступним чином:
Вищенаведене рівняння називають рівнянням Фішера. Запишемо його в літерному позначенні:
1 + r = (1 + y)*(1 + i) (3.44) де: r - номінальна ставка відсотку; у - реальна ставка відсотку; і - темп інфляції. З рівняння (39) можна одержати реальну відсоткову ставку:
|

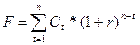 (3.27)
(3.27)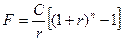 (3.28)
(3.28)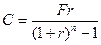 (3.29)
(3.29)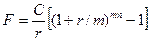 (3.30)
(3.30) (3.31)
(3.31) (3.32)
(3.32)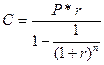 (3.33)
(3.33)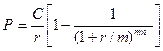 (3.34)
(3.34) (3.35)
(3.35)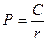 (3.36)
(3.36)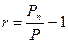 (3.37)
(3.37)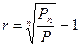 (3.38)
(3.38)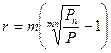 (3.39)
(3.39)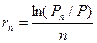 (3.40)
(3.40) або
або 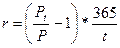 (3.41)
(3.41) (3.42)
(3.42)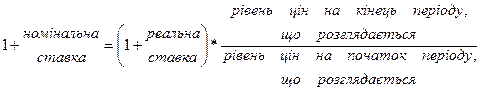 (3.43)
(3.43)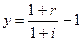 або
або 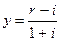 (3.45)
(3.45)


