Складний відсоток.
Нарахування відсотку один раз на рік. У довгострокових фінансово-кредитних угодах частіше використовують нарахування складних відсотків. При нарахуванні складних відсотків їх нараховують не тільки на основну суму, а й на суму, що включає як основну суму, так і нараховані раніше відсотки. У цьому випадку кажуть, що відбувається капіталізація відсотків в міру їх нарахування. При нарахуванні складних відсотків за перший період базою для нарахування є основна сума:
Рt = Р * (1 + r) (3.12)
Відмінність результатів при складному і простому відсотків виникає, починаючи з другого періоду нарахування, а через n років сума на рахунку зросте до величини:
Рn = Р * (1 + r)n (3.13)
Нарахування відсотків декілька разів на рік. Складний відсоток може нараховуватися частіше, ніж один раз на рік, наприклад, раз в півроку, квартал, місяць тощо. Нарахування складних відсотків декілька разів на рік називаєтьсякомпаундингом. Відсотки, що нараховуються з певною періодичністю, називаються дискретними. Нарощена сума буде розраховуватись за наступною формулою:
де: m - періодичність нарахування відсотку протягом року. Із зростанням кількості нарахувань відсотків протягом року абсолютний річний доход інвестора зростає. Безперервне нарахування відсотку. Якщо тривалість інтервалу нарахування наближається до нуля, а періодичність нарахування відсотків - до нескінченності (m → ∞), ми одержимо безперервне нарахування відсотків, яке нерідко використовується в світовій практиці. Іншими словами, безперервне нарахування відсотків називається нескінченним компаундингом. Формула для нескінченно нараховуваного відсотку має наступний вигляд:
де: rn - відсоток, що нараховується безперервно; n - період часу нарахування відсотку; е- 2,71828... Еквівалентний і ефективний відсотки. В практиці фінансового ринку відсоток, що нараховується по активу, задають як простий відсоток з розрахунку на рік. Однак, якщо в рамках року по активу передбачено нарахування складного відсотку, то загальний результат, який одержить інвестор, буде вище декларованого. Щоб його визначити, необхідно розрахувати ефективний або реальний відсоток. Ефективний (реальний) відсоток - це відсоток, який реально одержує інвестор за результатами року при нарахуванні складного відсотку. Ефективний відсоток можна визначити з наступного співвідношення:
де: rеф - ефективний відсоток; r - простий відсоток з розрахунку на рік, який заданий за умовами фінансового інструменту. Поєднання простого і складного відсотків. Досить часто фінансові контракти укладаються на період, що відрізняється від цілої кількості років. В даному випадку відсотки можуть нараховуватися або за схемою складних відсотків або за наступною схемою:
де: Pn+t – сума, яку одержить інвестор за n років і t днів; Р – початково інвестована сума; t – число днів, за які нараховується простий відсоток; r – відсоток, що нараховується протягом року.
Необхідно враховувати, що даний метод дає менший, ніж потрібно результат. Отже, в ситуації, коли номінали грошових сум досить високі, цей метод не використовується. В цьому разі застосовують наступні формули (3.18) і (3.19) (капіталізація відсотків здійснюється щорічно):
Дисконтована вартість. У фінансових розрахунках виникає необхідність порівнювати між собою різні суми грошей в різні моменти часу. Дисконтування – це зведення економічних показників різних років до порівняного в часі вигляду. Дисконтування здійснюється за допомогою коефіцієнта дисконтування (дисконтую чого множника). Цю задачу вирішують за допомогою наступної формули:
де: Рn – це майбутня вартість; Р – дисконтована або приведена вартість (синонімами є сьогоднішня, дійсна, поточна вартість);
Формула використовується також при оцінці облігацій з нульовим купоном. При нарахуванні складного відсотку m разів на рік формула (15) набуває вигляду:
Для відсотку, що нараховується безперервно:
Для розрахунку дисконтованої вартості для простого відсотку використовується формула:
Визначення періоду нарахування відсотків. На практиці виникають питання визначення періоду часу, який необхідний для збільшення суми Р до значення Рn при нарахуванні відсотку r. Для простого відсотку:
Період t буде дорівнювати відповідно:
Період часу інвестування при складному відсотку дорівнює:
|

 (3.14)
(3.14) (3.15)
(3.15)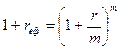 →
→  (3.16)
(3.16) (3.17)
(3.17) (3.18)
(3.18)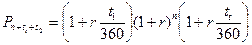 (3.19)
(3.19) (3.20)
(3.20) - це коефіцієнт дисконтування - його величина відповідає поточній вартості однієї грошової одиниці, яка буде одержана в кінці періоду n при складному відсотку r. Його величина залежить від тривалості свого періоду і необхідної ставки дисконту.
- це коефіцієнт дисконтування - його величина відповідає поточній вартості однієї грошової одиниці, яка буде одержана в кінці періоду n при складному відсотку r. Його величина залежить від тривалості свого періоду і необхідної ставки дисконту.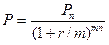 (3.21)
(3.21)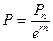 (3.22)
(3.22) (3.23)
(3.23) (3.24)
(3.24) (3.25)
(3.25) (3.26)
(3.26)


