Коэффициенты взаимной сопряженности Чупрова (K) и Пирсона (С)
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона-Чупрова. Коэффициент Чупрова (К) – тетрахорический коэффициент корреляции для дихотомических переменных, основанных на нормальных распределениях. Его иногда называют коэффициентом среднеквадратической сопряженности Чупрова.
К =
Коэффициент Пирсона (С) для дихотомических данных применяется в тех случаях, когда совпадает количество строк и количество столбцов.
С =
где φ2 – показатель взаимной сопряженности; φ2 определяется как сумма отношений квадратов частот каждой клетки к произведению итоговых частот соответствующего столбца и строки. Вычитая из этой суммы 1, получаем величину φ2:
k 1 – число значений (групп) первого признака; k 2 – число значений (групп) второго признака. Чем ближе величины С и К к 1, тем теснее связь. Для расчета коэффициента взаимной сопряженности составляется вспомогательная таблица (табл. 10).
Таблица 10 Вспомогательная таблица для расчета коэффициента
1 + φ 2 =
Например, по данным наблюдения нам нужно определить, существует ли у людей сопряженность между цветом волос и цветом глаз. В табл. 11 приведены частоты совместного распределения трех градаций цвета глаз и четырех градаций цвета волос.
Таблица 11 Сопряженность между цветом волос и цветом глаз
1 + φ2 =0,49 + 0,49 + 0,17 = 1,15; φ2 =0,15;
По одной из формул вычислим коэффициент взаимной сопряженности Пирсона: С ≈ 0,36. Коэффициент Чупрова дает несколько меньшую величину: К ≈ 0,25. Коэффициент Чупрова менее, чем коэффициент Пирсона, чувствителен к количеству событий m х n, поэтому при малых значениях m х n лучше применять коэффициент К. Отметим, что оба коэффициента изменяются только от нуля до единицы и измеряют тесноту сопряженности, не указывая ее направления, о котором легко судить по форме совместного распределения вероятностей (частот) событий.
|

 при k1 ≠ k2.
при k1 ≠ k2. ,
,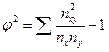 ;
;







