МЕРЫ СВЯЗИ В ШКАЛЕ РАНГОВ
3.1. Коэффициент ранговой корреляции Спирмена (rs)
В анализе социально-психологических явлений часто приходится прибегать к различным условным оценкам, например рангам, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Ранжирование – это процедура упорядочения объектов исследования, которое выполняется на основе предпочтения, а ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Коэффициент ранговой корреляции Cпирмена rs – коэффициент, который измеряет связь между рангами (местами) данной варианты по разным признакам, но не между собственными величинами варианты. Коэффициент Спирмена используется для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака. Коэффициент корреляции рангов (Спирмена) рассчитывается по формуле rs = 1- где: n – объем совокупности, длина одного статистического ряда; Xi – Yi – это разность между рангами i -го объекта. Коэффициент Спирмена принимает любые значения в интервале [-1; 1]. В качестве примера ранжирования можно привести возможность упорядочения оценок учащихся выпускных классов. Для каждого из 500 учащихся вычисляются средние баллы. Затем Пример вычисления коэффициента Спирмена приведен в табл. 12.
Таблица 12 Два множества рангов, присвоенных экспертом 12 учащимся по неприязни
Предположим, что 12 учащихся ранжируются одним экспертом по их открытой неприязни к преподавателю (X) и к другим учащимся (Y). Ранг 1 дается учащемуся, проявляющему наибольшую неприязнь к преподавателю; ранг 12 указывает учащегося, который показал себя наименее враждебным. Аналогичная процедура ранжирования используется для оценки неприязни к соученикам. Гипотетические данные приводятся в табл. 12. Учащийся А был по рангу вторым по открытой неприязни к преподавателю Х и шестым по отношению к другим учащимся Y. Очевидный способ описания связи между двумя последовательностями рангов (Х и Y) состоит в том, чтобы вычислить коэффициент корреляции Спирмена. Заметьте, что в табл. 12 ΣX = ΣY и ΣX2 = ΣY2. Следует сразу же отметить, что эти равенства верны, пока ранги не связаны. Можно показать, что ΣX = 1 + 2 + …+ n =
По табл. 12 имеем
rs = 1 –
rs = 1 –
Значение rs свидетельствует о довольно сильной прямой связи между открытой неприязнью учащихся к преподавателю и к другим учащимся.
|

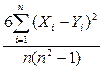 ,
, .
.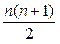 = 78;
= 78;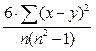 ;
;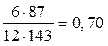 .
.


