Другие коэффициенты
Для ситуации, когда Х – дихотомия, основанная на нормальном распределении, a Y измерен в шкале порядка, подходят только коэффициенты, которые были введены Кертеном (1956) и Глассом (1966). При измерениях такого рода, мы исходим из гипотезы о нормальном распределении, лежащем в основе дихотомии для X, и обращаемся к вычислению бисериального рангового коэффициента корреляции Кертена, который обсуждается ниже в п. 5.3. Мера связи, когда одна переменная измеряется дихотомически на основе нормального распределения, а другая – в шкале интервалов или отношений, – это бисериальный коэффициент корреляции rbis. Предположим, что переменная Y измеряется дихотомически, хотя более тщательная или более совершенная методика могла бы дать приблизительно нормальное распределение значений Y. Мы говорим, что измерение Y привело к дихотомии, основанной на нормальном распределении. Таким образом, Y измеряется точно тем же способом, что и переменные, участвующие в вычислении тетрахорического коэффициента корреляции. Однако в этом случае данные измерений Х надо рассматривать как значения в шкале интервалов или отношений, которые распределены приблизительно нормально. Например, значения Х могут быть результатами теста на симпатии и антипатии учащихся к педагогам, а Y, принимающий значения 0 и 1, – результатами ответа на вопросы, оценивающие усвоение знаний. При более тщательно разработанных проверках успеваемости можно было бы обеспечить более широкий диапазон оценок успеваемости (оценок Y), которые были бы распределены приблизительно нормально. Тогда два массива нормально распределенных данных для Х и Y привели бы к определению rху. Что же говорят о величине rху оценки Х и дихотомические оценки Y? Ответ на этот вопрос дает бисериальный коэффициент корреляции rbis. Бисериальный коэффициент корреляции – это корреляция произведения моментов между Х и нормально распределенными значениями Y, что, по предположению, лежит в основе дихотомии Допустим, что преподаватель хочет установить связь времени (X), затраченного учащимися на изучение уравнивания химических реакций, и их навыками (Y) уравнивания таких реакций. Измерения значения Х ведутся по данным сообщений учащихся о времени, необходимом для выполнения домашнего задания. Вероятно, Y можно было оценить при более основательной проверке успеваемости так, чтобы обеспечивалось приблизительно нормальное распределение; но допустим, что время, которым располагал преподаватель, позволяет предложить учащимся рассмотреть только один вопрос — химическую реакцию для уравнивания. Поэтому предполагается, что в основе нулевых (неверный ответ) и единичных (правильное решение) лежит нормальное распределение ответов. Данные, которые можно было бы получить в результате такого исследования, приводятся в табл. 20. Они показывают, что 11 из 18 учащихся верно выполнили задание и их оценки в среднем более высоки, чем у 7 учащихся, которые решили задачу неправильно. Объяснение, на основе которого выводится rbis, следует из теории регрессии. Коэффициент регрессии для предсказания Х по нормально распределенному Y есть:
где sy – стандартное отклонение гипотетически нормально распределенного Y, причем Y – не дихотомическая переменная. Наклон линии регрессии для предсказания Х по Y можно аппроксимировать наклоном линии, проходящей через среднее значение Х для объектов, имеющих нули по Y (обозначим их Таблица 20 Пример вычисления бисериального коэффициента корреляции
Наклон этой линии равен разности ( rbis = где Пример вычисления rbis приведен в табл. 20. Вычисление rbis можно упростить, пользуясь следующей эквивалентной, но слегка отличаю-щейся формулой, позволяющей получать то же, что и предыдущее уравнение:
rbis =
В отличие от любого другого коэффициента корреляции, rbis иногда может принимать значения ниже –1 и выше +1. Но это лишь означает, что либо некорректно предположение о нормальности распределения X, либо что имеет место флуктуация выборки, когда значение n мало, что приводит к распределению значений Х в выборке с эксцессом меньше нормального. Вероятно, вы уже заметили, что данные, по которым вычислялись и точечно-бисериальный коэффициент корреляции rpb и rbis, похожи. Единственная разница между постановками двух задач состоит в том, что в случае rbis выдвигаются некоторые гипотезы относительно распределения, лежащего в основе дихотомии. В том, что касается свойств данных, rpb и rbis существенно различны. Поэтому беспредметны вопросы типа: «Как сравнить rpb и rbis для одной совокупности данных?» Области применения коэффициентов не пересекаются: каждый соответствует своей цели. Для одних и тех же данных отношение rpb и rbis равно
Минимальная величина отношения в этом уравнении есть 1,25, когда ни rbis, ни rpb не равны нулю. Поэтому, если rpb положительно, rbis будет положительным и большим; если rpb отрицательно, rbis будет отрицательным и ближе к –1. Если rpb равно нулю, то rbis также равен нулю. Таким образом, одни и те же данные дают основание для фиксации более сильной связи между Х и Y, если относительно нее делается больше предположений, т.е. если допустить, что дихотомия основана на нормальном распределении. Понятия, лежащие в основе бисериальной корреляции, можно обобщить для применения при определении (установлении) трисериальной и полисериальной корреляции. Если значения Y измеряются трихотомически (О, 1, 2), можно использовать трисериальный коэффициент корреляции для оценки корреляции произведения моментов между Х и нормально распределенным Y, который, по предположению, трихотомичен. Обобщение rbis до полисериальной корреляции содержится в работе Джаспена (1946). Практика свидетельствует о том, что часто величина коэффициента полисериальной корреляции намного отличается от величины rbis , которая была бы получена при объединении нескольких категорий в две (так, например, при замене трихотомической переменной на дихотомическую переменную совмещением двух смежных категорий).
5.3. Бисериальная ранговая корреляция rbis
Коэффициент бисериальной ранговой корреляции тесно связан с τ Кендалла, в определении используются понятия совпадения и инверсии. Обозначим его как рангово-бисериальный коэффициент rb. Пусть Х дихотомическая переменная, а Y – переменная, имеющая n рангов 1, 2,..., n. Кертен искал такой коэффициент, описывающий связь между Х и Y, чтобы: а) при любых условиях он мог достигнуть границы +1; б) был бы равен +1, когда все n наивысших рангов являются единицами по дихотомии; в) был бы строго непараметричным, т.е. полностью определимым в терминах инверсий и совпадений без использования таких понятий, как среднее, дисперсия, регрессия и т.д. Гласс (1966) показал, что rb алгебраически эквивалентен коэффициенту для порядковых переменных. Практическое значение этого факта заключается в том, что появляется простой способ вычисления rb без подсчета совпадений и инверсий, но используют Fi – средний ранг объектов, имеющих 1 по X; a Fo – средний ранг объектов с 0 по X. Уайтфилд (1947) вывел коэффициент корреляции одной дихотомической и одной порядковой переменной. Его подход сводился к тому, чтобы рассматривать дихотомическую переменную как ранжируемую переменную, связанную на двух рангах. Далее он применил формулу τ Кендалла для связанных рангов. Получившийся коэффициент имеет тот же числитель, что и rb, но другой знаменатель. В качестве меры корреляции предпочтительнее рангово-бисериальный коэффициент, поскольку коэффициент Уайтфилда не достигает +1, когда между Х и Y существуют некоторые строгие взаимосвязи.
|

 ,
, ), и среднее Х для объектов, имеющих единицы по Y (обозначим их
), и среднее Х для объектов, имеющих единицы по Y (обозначим их  ). Такая линия проведена на диаграмме рассеивания в табл. 20. Это линия наименьших квадратов в том смысле, что среднее группы представляет собой точку, относительно которой сумма квадратов отклонений минимальна.
). Такая линия проведена на диаграмме рассеивания в табл. 20. Это линия наименьших квадратов в том смысле, что среднее группы представляет собой точку, относительно которой сумма квадратов отклонений минимальна. n1 =11, n0 = 7, n = 18
n1 =11, n0 = 7, n = 18
 = 11,44,
Sx = 2,55, u = 0,3836,
rbis = 0,60
= 11,44,
Sx = 2,55, u = 0,3836,
rbis = 0,60
 1 –
1 –  ,
, и
и  являются средними значениями Х для объектов, имеющих соответственно единицы и нули по Y; sx – стандартное отклонение значений X; n1 и n0 – число единиц и нулей для Y, соответственно (n1 + n0 = n); и u — ордината (т.е. высота) нормированного нормального распределения в точке, за которой лежит 100 – (n1/n) процентов площади под кривой (см. рис. 3).
являются средними значениями Х для объектов, имеющих соответственно единицы и нули по Y; sx – стандартное отклонение значений X; n1 и n0 – число единиц и нулей для Y, соответственно (n1 + n0 = n); и u — ордината (т.е. высота) нормированного нормального распределения в точке, за которой лежит 100 – (n1/n) процентов площади под кривой (см. рис. 3). .
.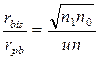 .
.


