Линейная регрессия как инструмент прогнозирования
В психологической практике часто встречаются нелинейная и квазилинейная модель регрессии. Главные отличия модели линейной регрессии от мер связи. Коэффициент корреляции позволяет установить отношение между психологическими переменными, т.е. наличие и степень связи между ними. Например, узнать, что существует зависимость между эффективностью деятельности и силой мотивации. Корреляционное отношение – мера линейной или нелинейной связи Х и Y. А с помощью модели линейной регрессии мы можем пойти дальше, т.е. предсказывать по значениям, отражающим силу мотивов, возможную (вероятную) эффективность деятельности личности. В принципе, модель простой линейной регрессии предполагает только две психологические переменные, в то время как могут существовать множественные модели линейной регрессии. Направления применения модели линейной регрессии в психологических исследованиях. 1. Приближенное аналитическое (формульное) выражение зависимости между психологи-ческими переменными, благодаря чему: - становится возможным определение значения интересующей нас психологической переменной, не изучавшейся ранее экспериментально; - найденные зависимости между психологическими переменными приобретут законченную математическую форму. 2. Модели линейной регрессии широко используются в целом ряде статистических процедур, активно применяемых при исследовании системы психологических переменных, в частности, модель линейной регрессии лежит в основе факторного, дисперсионного, регрессионного анализов. Применение модели линейной регрессии основывается на корректной процедуре первичного измерения психологических переменных. Области применения модели линейной регрессии: Прогнозирование, диагностика социально-психологических характеристик коллективов. В данном случае модель линейной регрессии выступает в качестве основы модели прогноза. Анализ результатов деятельности (индивидуальных или групповых).
6.3. Математический и графический расчет формулы линейной регрессии.
Расчет линейной регрессии включает действия: · построение уравнения регрессии; · оценку регрессии; · анализ. Когда исследователь наблюдает две психологические переменные, он может изобразить их графически и найти между ними корреляцию; причем графически надо найти аппроксимирующую кривую, которая описывает взаимосвязь между Х и У (линейная, логарифмическая и т.д.). Тогда полученную кривую можно использовать для предсказания значений Х по очередному результату У (и наоборот). Выбор аппроксимирующей функции во многом определяется подготовкой исследования и представляет собой своего рода искусство. Аппроксимация простой регрессии – приближенное аналитическое (формульное) выражение регрессии по ряду пар значений Х и Y, полученных в эксперименте. Для построения аппроксимирующей функции решающую роль играют априорные знания о законе, связывающем те или иные психологические переменные. Например, для времени (t) реакции – гипербола, для интенсивности ощущений – логарифмическая или степенная зависимость. Значительную роль в поиске аппроксимирующей функции играют машинные методы. Для построения графика используется стандартный метод – т.е. метод наименьших квадратов, а сама линия, построенная по этому методу, называется линией регрессии (убывания). Линия регрессии– линия, построенная по средним значениям первого признака (зависимой переменной) с соответствующим средним интервалом признаков-факторов (независимой переменной). Регрессия (парная) характеризует связь между двумя признаками: результативным и факторным. Аналитическая связь между ними описывается уравнениями: прямой у = а0 + а1х; гиперболы у = а0 + а1/х; параболы у = а0 + а1х + а2х2 и т.д. Определить тип уравнения регрессии можно, исследуя зависимость графически. Однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково – примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи – гиперболическая. Если факторный признак увеличивается в арифметической прогрессии, а результативный – значительно быстрее, то используется параболическая, или степенная регрессия. Оценка параметров уравнений регрессии (а0, а1 и а2) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Различают регрессии линейные и нелинейные (рис. 8).
а) линейная регрессия б) параболическая регрессия
Рис. 8. Графики линейной и параболической регрессии
Наибольшее распространение имеет модель линейной регрессии, которую можно представить в виде уравнения регрессии. Уравнение регрессии – некоторое аналитическое выражение, которое представляет варьирующие значения функции. Для простой линейной регрессии уравнение имеет вид:
где b – свободный член, характеризующий значение уi, при условии хi = 0, а – коэффициент регрессии, характеризующий скорость изменения уi в зависимости от изменения хi. Коэффициент регрессии – мера, характеризующая скорость изменения средних значений одной случайной величины при изменении другой. Величина а (коэффициент регрессии) выступает показателем “крутости” изменений функции (угла наклона выравнивающей прямой к оси абсцисс). Коэффициент регрессии позволяет рассчитать, насколько в среднем изменится признак при изменении на единицу меры другого, связанного с ним признака. а – численно равен tg a, т.е., а = tg a=Dуi/D хi. Графически изображение уравнения линейной регрессии приведено на рис. 9.
Рис. 9. Графическое изображение уравнения линейной регрессии Особенности модели линейной регрессии: 1) двойной характер предсказания: - можно предсказывать У/Х (У по Х), - можно предсказывать Х/У; 2) наличие ошибки оценивания. Понятие ошибки является очень важным для практического построения модели линейной регрессии. Ошибка оценки ei – разность между фактическим значением Y объекта и значением уi ≈ уi; еi = уi – тогда уi = Строить линию регрессии можно двумя способами: методом наименьших квадратов и графическим методом.
|


 = ахi + b,
= ахi + b,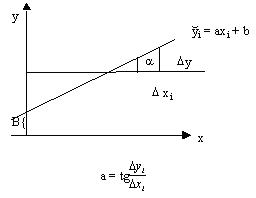
 , которое мы предсказываем для него. Стандартная ошибка оценки se – положительное значение квадратного корня из дисперсии ошибки оценки.
, которое мы предсказываем для него. Стандартная ошибка оценки se – положительное значение квадратного корня из дисперсии ошибки оценки. ;
;


