Построение уравнения регрессии
Различают регрессии: линейные и нелинейные. Линейная зависимость в регрессионном анализе описывается формулой: y x= ax + b. Степенная регрессия: yx= a xв Экспоненциальная регрессия: y x=exp(ax + b) Гипербола: Коэффициент b – свободный член уравнения, выражает действие неучтенных факторов. Например, говорит о том, что какие-то признаки (факторы) в изучаемом явлении нами не учтены. Коэффициент a показывает связь зависимой переменной с независимой переменной, например, с изменением независимой переменной на единицу, зависимая переменная растет на величину коэффициента a (для данной выборки и в данное время). Расчет параметров уравнения регрессии решается с помощью системы двух уравнений: bn + a Σ x = Σ y; b Σ x + a Σ x2 = Σx y. Для решения системы проводим расчет коэффициентов регрессии по формуле:
Например, требуется оценить (предсказать) зависимость качества работы оператора yi от скорости работы xi. Данные и вычисления проведены с помощью табл. 21.
Таблица 21 Результаты вычислений зависимости качества работы оператора от скорости работы
Подставляя значения a и b получаем уравнение: у = b + aх y = 2,54 + 0,32x Стандартная ошибка оценки: Оценка уравнения. Для проверки правильности расчетов в полученное уравнение подставляем Если параметры найдены верно, то получим
Подставляя в полученное уравнение эмпирические данные по независимой переменной – значения x i, найдем расчетные (теоретические) значения изучаемого признака yi (обозначим
что близко к эмпирическим значениям. Расчетные данные дают нам возможность прогноза величины исследуемого признака (среднего его значения) при сохранении условий на генеральной совокупности. Показатели регрессии, как и всякие другие выборочные показатели, являются случайными величинами. Их значения могут не совпадать с соответствующими значениями в генеральной совокупности. Для измерения возможной погрешности, с какой определяются выборочные показатели относительно своих генеральных параметров, служат ошибки репрезентативности, позволяющие с той или иной вероятностью устанавливать доверительные границы для генеральных параметров по данным выборочных наблюдений, оценивать статистическую достоверность показателей регрессии. Достоверность коэффициента регрессии оценивается по критерию Стьюдента t с числом степеней свободы К = n - 2. Значимость самого уравнения регрессии оценивается с помощью Анализ уравнения регрессии. Коэффициент регрессии b =0,32 показывает, что при увеличении скорости работы на единицу в среднем 2,5 ошибки являются результатом неучтенных в уравнении факторов. Поскольку среднее число ошибок y = 4,2, то это составит более 60% всех ошибок, остальные (около 40%) объясняются учтенным фактором, т.е. скоростью работы. Окончательный вывод о предсказательной возможности уравнения регрессии можно сделать по показателю тесноты связи – в данном случае по коэффициенту корреляции rxy и коэффициенту детерминации Коэффициент детерминации, умноженный на 100%, дает возможность говорить, какая доля роста всех ошибок объясняется переменной Х. Следовательно, 36% всех ошибок объясняются скоростью работы, 64% – другими факторами. Практический вывод из анализа: регулирование темпа работы не затрагивает почти две трети возможных ошибок. Следует проанализировать влияние на качество таких факторов, как условия работы, квалификация, стимулирование и т.д.
|

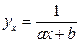 .
.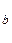
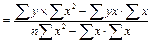 ,
,
 .
.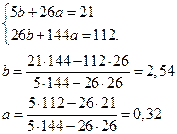 y = 2,54 + 0,32x
y = 2,54 + 0,32x
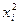 = 144
= 144

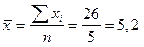 . Подставляя значения a в уравнение регрессии, проверяем полученное уравнение; если расчеты правильные, то мы должны получить yср для данной выборки.
. Подставляя значения a в уравнение регрессии, проверяем полученное уравнение; если расчеты правильные, то мы должны получить yср для данной выборки. ,
,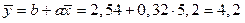 .
.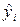 ). Для нашего примера
). Для нашего примера



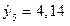 ,
,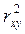 . Для данного примера rxy = 0,6;
. Для данного примера rxy = 0,6;  Коэффициент корреляции позволяет объяснить рост изучаемой переменной У на коэффициент 0,6 в зависимости от переменной Х.
Коэффициент корреляции позволяет объяснить рост изучаемой переменной У на коэффициент 0,6 в зависимости от переменной Х.


