Доказательство
Необходимость. (Þ) Покажем, что если U t 1 = U t 2, то образцы t 1 и t 2 совпадают с точностью до переименования переменных. Пусть U t 1 = U t 2. Без ограничения общности можно считать, что множества символов переменных в образцах t 1 и t 2 не пересекаются. Длины слов t 1 и t 2 совпадают. Действительно, всякое применение произвольного образца, получаемое заменой символов переменных на слова, состоящие из одного символа, имеет длину, равную длине самого образца. Поэтому если бы длины образцов t 1 и t 2 были разными, то множество применений более короткого образца содержало бы слова, не входящие во множество применений другого образца. Пусть t 1 = s1,..., s k и t 2 = d1,..., d k. Произведем последовательное посимвольное сравнение t 1 и t 2слева направо. При этом возможны следующие случаи: 1) s i Î (А 2) s i Î V.
Рассмотрим первый из этих случаев и покажем, что справедливы соотношения d i Î (А Для этого рассмотрим множества всех таких применений t 1 и t 2, которые получаются из t 1 и t 2 заменой символов переменных на слова длины 1. Тогда, если d i Из проведенных рассуждений следует, что на одинаковых позициях образцов t 1 и t 2 могут располагаться либо символы переменных, либо равные символы из А
Рассмотрим второй случай. Покажем, что в этом случае d i также является символом переменной и s i = s j тогда и только тогда, когда d i = d j. Первое из приведенных свойств верно, поскольку если d i Î А Проверим справедливость второго свойства. Пусть s i Î V и s j, j < i,обозначают одну и ту же переменную в t 1. Тогда все применения t 1, получаемые заменой переменных на слова длины 1 в алфавите А È B, имеют одинаковые j -й и i -й символы. Если же d i и d j - разные символы переменных в t 2, то среди кратчайших по длине применений образца t 1 имеются такие, в которых j -й и i -й символы - разные. Поэтому U t 1 ¹ U t 2. Последнее заключение противоречит предполагаемому равенству множеств U t 1 и U t 2. Доказательство того, что если d i = d j, то s i = s j можно провести аналогичными рассуждениями. Из доказательства свойств, имеющих место в случаях 1 и 2, следует, что t 1 и t 1 совпадают с точностью до переименования переменных. Достаточность. (Ü) Пусть образцы t 1 и t 2 совпадают с точностью до переименования переменных. Тогда множества применений этих образцов совпадают. Действительно, пусть подстановка Q 1 = Тогда, если слово Следовательно, U t 1 = U t 2.
|

 B);
B);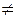 s i, то рассматриваемые множества кратчайших по длине слов в U t 1 и U t 2 являются разными, так как i -й символ всех слов первого множества равен s i. Однако значения i -го символа слов второго множества могут быть отличными от s i.
s i, то рассматриваемые множества кратчайших по длине слов в U t 1 и U t 2 являются разными, так как i -й символ всех слов первого множества равен s i. Однако значения i -го символа слов второго множества могут быть отличными от s i. задает переименование переменных из t 1 в переменные из t 2, которое преобразует t 1 в t 2.
задает переименование переменных из t 1 в переменные из t 2, которое преобразует t 1 в t 2.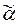 является применением t 1, получаемым с помощью подстановки p, то
является применением t 1, получаемым с помощью подстановки p, то 


