СИСТЕМАХВыводы в системах Поста и множества выводимых слов обладают рядом интересных и важных свойств. 1. Существует алгоритм, который по произвольным словам в основном и вспомогательном алфавитах Возможен следующий алгоритм определения применимости произвольной продукции p к заданным словам 1.1. Выделяются все различные символы переменных в образцах t 1,..., t k+ 1. 1.2. Находится длина d самого короткого слова среди слов 1.3. Для выделенного множества символов переменных строятся все подстановки, в которых эти переменные заменяются такими словами в основном и вспомогательном алфавитах, длина которых не превосходит d. 1.4. Для каждой подстановки Q проверяется условие: " i = 1,..., k + 1 ( 1.5. Если условие (1) имеет место хотя бы для одной подстановки, то 1.6. Если для всех подстановок условие (1) не выполняется, то 2. Существует алгоритм, который по произвольной последовательности Пример соответствующего алгоритма может быть получен на основе схемы предыдущего алгоритма. 3. Множество различных слов, которые могут быть получены из слов
|
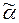1,..., 
определяет выводимость слова 
