СИСТЕМАХ. Задачи, которые можно решать получать с помощью систем Поста, естественно связаны с множествами слов
Задачи, которые можно решать получать с помощью систем Поста, естественно связаны с множествами слов, выводимых в этих системах. Простейший вопрос, который можно отнести к системе P - это вопрос о принадлежности конкретного слова множеству слов W P, выводимых в P. Такой вопрос записывается в виде: ″ Ответом на него может быть только либо нет, либо да. Естественный процесс поиска правильного ответа на этот вопрос состоит в нахождении вывода слова При этом если существует такой вывод W, то он может быть найден последовательным перебором всех конечных выводов в системе P. Если же такой вывод отсутствует, а значит, слово Обобщение рассмотренного типа задач, решаемых системами Поста, - это задачи, связанные с вопросом о выводимости в системе P слов, являющихся применениями заданного образца. Для заданного образца t требуется получить ответ на вопрос о существовании такой подстановки Q, что t Q ÎW P. Поскольку W P может содержать несколько различных применений t, то возможны несколько вариантов уточнения данного типа вопроса:
1) найти любое применение t, выводимое в системе P; 2) перечислить все применения t, выводимые в системе P; 3) найти применения t, обладающие дополнительным свойством. Ответы на перечисленные варианты вопроса естественно представлять в виде последовательностей таких подстановок, что применение подстановки к t дает один из элементов ответа на вопрос. Если же ни одно применение t не выводимо в системе Поста P, то ответом на поставленный вопрос является нет. Как и в предыдущем случае, естественный алгоритм перебора всех конечных выводов в системе P не позволяет получить отрицательный ответ.
|

 ÎW P ″?
ÎW P ″?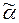 в системе P.
в системе P.


