ПРОДУКЦИИ И СИСТЕМЫ ПОСТА
ПРОДУКЦИОННЫЕ СИСТЕМЫ
Рассмотрим еще одну формальную модель, в которой уточняется понятие алгоритма и вычислимой функции. Такая модель имеет разнообразные практические приложения и отличается от модели рекурсивных функций по способам представления алгоритмов и механизму их выполнения, но функционально эквивалентна ей. Эта формализация лежит в основе современного логического программирования и моделей алгоритмов символьной обработки.
Пусть А, B и V - три непересекающихся конечных алфавита, причем В дальнейшем всегда будет предполагаться, что | А È B | ³ 2. Всякое слово, составленное из символов алфавитов А, B и V, называется образцом. Слово Применение подстановки Q к образцу t обозначается как tQ. Всякий образец представляет собой структурное описание множества всех своих применений, т.е. множества слов, строение которых задается образцом. Например, если A = { 0, 1 }, B = Различные образцы соответствуют различным классам слов, структура которых описывается этими образцами. Такое свойство следует из следующего утверждения.
|
А È B ¹Æ, которые называются соответственно основным алфавитом, вспомогательным алфавитом и алфавитом переменных.
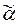Î(A È B)* называется применением образца t, если существует подстановка Q = 
, где x 1,..., x k - все различные символы переменных, входящих в t, а 
B, что слово 
, V = { x }, то образец t = 1 x 0 представляет все правильные записи не менее чем трехразрядных четных двоичных чисел. Образец x 1 x представляет двоичные последовательности, составленные из двух одинаковых последовательностей разделенных 1.
