Доказательство. Пусть R и Q - символы, которые не встречаются среди символов алфавитов систем P1 и P2.
Пусть R и Q - символы, которые не встречаются среди символов алфавитов систем P 1 и P 2. 1. Определим систему PU. Основной алфавит и алфавит переменных этой системы получаются объединениями основных алфавитов и алфавитов переменных систем P 1 и P 2. Вспомогательный алфавит системы PU состоит из символов вспомогательных алфавитов для P 1 и P 2, а также символов R и Q. Множество продукций системы PU состоит из продукций, получаемых из продукций P 1 приписыванием всем образцам слева символа R, а также продукций, получаемых из продукций системы P 2 с помощью аналогичного приписывания символа Q. Кроме того, в PU добавлены продукции:
Покажем, что в системе PU выводятся те и только те слова, которые принадлежат W 1 Это следует из того, что некоторое слово x выводится в системе PU тогда и только тогда, когда в этой системе выводится либо слово Rx, либо слово Qx. Последнее равносильно тому, что x выводится либо в P 1, либо в P 2. Поэтому в PU выводится множество слов W 1
2. Определим систему Поста PI. Алфавиты этой системы определяются так же, как это было определено для системы PU. Продукции системы PI получаются из продукций P 1 и P 2 приписыванием ко всем образцам в них слева символов R и Q соответственно. К этим продукциям добавляется еще одна
Видно, что в системе PI выводятся такие и только такие слова x, которые могут быть выведены как в P 1, так и в P 2. Поэтому множество слов, выводимых в системе PI, равно
|

 и
и  .
. W 2.
W 2. 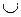 W 2.
W 2. .
. W 2.
W 2.


