Доказательство. Проведем доказательство сформулированной теоремы по этапам определения частично-рекурсивных функций.
Проведем доказательство сформулированной теоремы по этапам определения частично-рекурсивных функций. 1. Покажем, что все примитивные функциивычисляются системами Поста. Действительно, функция O (x) вычисляется с помощью продукции p: Функция S (x) вычисляется с помощью продукций p1 - p8, а
2. Покажем, что всякая суперпозиция функций, вычислимых системами Поста, вычисляется в некоторой системе Поста. Пусть заданы функции f (x 1,..., xn), j1(x 1,1,..., x 1, m 1),..., j n (xn ,1,..., xn , m n), которые вычисляются системами Поста P 0, P 1,..., P n соответственно. Покажем, что функция h (xi 1,..., xi k) = = f (j1(x 1,1,..., x 1, m 1),..., j n (xn ,1,..., xn , m n)), где xi 1,..., xi k- все различные переменные функций j1,..., j n, также вычислима некоторой системой Поста. Обозначим как G 0, G 1,..., G n - вспомогательные символы, которые не встречаются среди символов алфавитов систем Поста P 0, P 1,..., P n. Модифицируем продукции этих систем Поста, приписав всем образцам каждой продукции из P iслева символ G i. Рассмотрим систему Поста P, продукциями которой являются все модифицированные продукции систем P 0, P 1,..., P n, а также продукция
Очевидно, что P вычисляет функцию h.
3. Покажем, что всякая функция, выражаемая через функции, вычислимые системами Поста с помощью операции примитивной рекурсии, вычисляется некоторой системой Поста.
Пусть функция f выражается через функции g и h с помощью операции примитивной рекурсии
f (x 1,..., x n, 0) = g (x 1,..., x n) f (x 1,..., x n, y + 1) = h (x 1,..., x n, f (x 1,..., x n, y)).
Пусть функции g и h вычисляются системами Поста Pg и Ph. Возьмем два вспомогательных символа Gg и Gh, не встречающиеся среди символов алфавитов систем Pg и Ph. Модифицируем продукции систем Pg и Ph, приписывая всем образцам в них слева соответственно символы Gg и Gh. Рассмотрим систему Поста P f, в которую включим модифицированные продукции систем Pg и Ph, продукции системы, вычисляющей функцию S (x) = x + 1, помеченные еще одним вспомогательным символом Gs. Для этого символа также предполагаем, что он не встречается среди символов всех рассматриваемых систем Поста. Добавим к этим продукциям еще две
Нетрудно видеть, что такие продукции соответствуют соотношениям схемы примитивной рекурсии, а P f вычисляет функцию f.
4. Покажем, что если функция f выражается через функцию, вычислимую некоторой системой Поста, с помощью операции минимизации, то она также вычисляется некоторой системой Поста. Пусть f (x 1,..., xn+ 1) = m t (g (x 1,..., xn, t) = xn +1) и функция g (x 1,..., xn+ 1) вычисляется продукционной системой Pg. Построим систему Поста P f, которая вычисляет Включим в Pf продукции систем, вычисляющих функции S (x) и g (x 1,..., x n + 1), а также добавим к ним продукции такой системы Поста, в которой выводятся пары неравных целых неотрицательных чисел: x <> y. Построение такой системы предлагалось ранее в упражнении. Модифицируем такие продукции так, чтобы никакие слова, выводимые в одной системе, не могли использоваться в качестве посылок продукций других систем. Например, это можно сделать, приписывая образцам продукций разных систем разные вспомогательные символы.
Добавим к указанным продукциям новые продукции:
Эти продукции позволяют вычислять вспомогательную функцию
Для вычисления значений функции f используются следующие две продукции:
Построенная система Поста вычисляет функцию f. По определению, всякая частично-рекурсивная функция может быть выражена через простейшие функции с помощью конечного числа применений операций суперпозиции, примитивной рекурсии и минимизации. Поскольку все простейшие функции вычислимы системами Поста и применение перечисленных операций к функциям, вычислимым системами Поста, приводит к функциям, вычислимым такими системами, то теорема доказана.
|

 , добавленной к рассмотренным ранее продукциям p1 - p6, позволяющим выводить все правильные двоичные записи натуральных чисел.
, добавленной к рассмотренным ранее продукциям p1 - p6, позволяющим выводить все правильные двоичные записи натуральных чисел.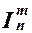 (x 1,..., xn) вычисляется с помощью дополнительной продукции
(x 1,..., xn) вычисляется с помощью дополнительной продукции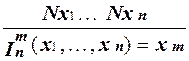 .
. .
.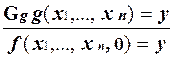 ; (1)
; (1)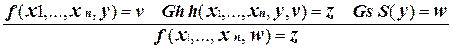 (2).
(2). (1)
(1)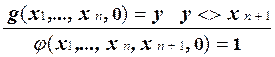 (2)
(2)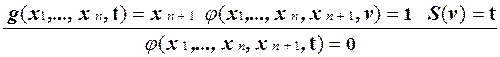 ; (3)
; (3)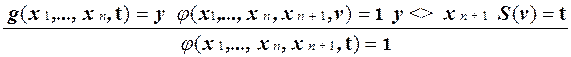 .(4)
.(4)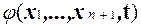 , которая принимает значение 0 только для такого наименьшего значения t, при котором
, которая принимает значение 0 только для такого наименьшего значения t, при котором 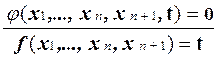 ; (5)
; (5)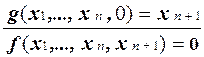 . (6)
. (6)


