СВОЙСТВА МНОЖЕСТВ ВЫВОДИМЫХ СЛОВ
Из всех слов, выводимых в произвольной системе Поста, выделяются подмножества таких слов, которые могут считаться окончательными результатами вычислений. В процессе вывода таких окончательных слов в системах Поста приходится использовать и другие слова, которые можно рассматривать как промежуточные или вспомогательные слова. В простейшем случае заключительными считаются все слова, которые не содержат символов вспомогательного алфавита. В других случаях заключительные слова должны иметь специальную структуру. Например, рассмотрим систему Поста, в которой выводятся все такие пары двоичных последовательностей (x, y), являющихся правильными записями неотрицательных целых чисел. В этой системе все выводимые слова, начинающиеся с буквы N, являются вспомогательными. Они представляют правильные записи целых неотрицательных чисел в двоичной системе, выводимых с помощью продукций:
p1 = N 0; p2 = N 1; p3 = N 11; p4 = N 10; p5 =
Пары целых неотрицательных чисел (x, y) выводятся с помощью продукции:
p7 =
Приведенная система Поста имеет основной алфавит Результатами в такой системе являются только такие выводимые слова, которые не содержат символа N. Выводимые в системе вспомогательные слова имеют вид Nx. Множество всех слов, выводимых в произвольной системе Поста с непустым вспомогательным алфавитом, разбивается на два класса: это класс слов, содержащих символы вспомогательного алфавита, и класс слов, состоящих только из символов основного алфавита. Слова из первого класса называются нетерминальными словами системы Поста; из второго класса - терминальными, или заключительными. В дальнейшем обозначение WP будет применяться для множества слов в основном алфавите, которые выводятся в системе Поста P. Другие слова, выводимые в системе Поста P и содержащие вспомогательные символы рассматриваются как промежуточные в выводах, позволяющие организовать вывод заключительных слов. Рассмотрим ещё один пример системы Поста, в которой выводятся все возможные пары слов вида ( Выпишем множество продукций соответствующей системы Поста. 1. Вспомогательные продукции, позволяющие выводить правильные двоичные записи неотрицательных целых чисел: p1= N 1; p2= N 0;p3= N 11; p4 = N 10; p5: 2. Вспомогательные продукции, позволяющие выводить слова вида S (x) = y, где x и y - это правильные двоичные записи неотрицательных целых чисел и у = x + 1: p7: S (0) = 1; p8: 3. Основные продукции, позволяющие выводить пары, слов ( p10: (0, 1); p11: (1, 1); p12: Здесь символы N и S образуют вспомогательный алфавит, а x, y, z - алфавит переменных. Остальные символы составляют основной алфавит.
Упражнение. Привести пример множества слов в алфавите { 0, 1 }, которое выводится только в таких системах Поста, которые имеют непустой вспомогательный алфавит.
Рассмотрим класс всех таких множеств слов, каждое из которых выводится в некоторой системе Поста. Покажем, что этот класс замкнут относительно операций объединения и пересечения множеств. Справедливость приведенного свойства вытекает из теоремы 9.2.
|

 ; p6 =
; p6 =  .
. .
.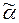 ,
,  ), где
), где  ; p9:
; p9:  .
. ; p13:
; p13:  .
.


