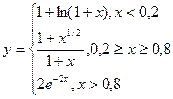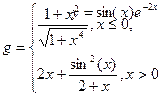Лабораторная работа №4

 

“Построение графиков функций и решение нелинейных уравнений в Microsoft Excel”

1 Цель работы:ознакомление с методами решения двух типичных задач: построения графиков и решения уравнений с одним неизвестным с помощью электронных таблиц. Для построения графиков Excel предоставляет прекрасное средство — мастер диаграмм с большим набором графиков и диаграмм, по­зволяющий представить данные наглядно, в наиболее выгодном свете.

2 Основные теоретические положения и методика выполнения работы

2.1 Построение графика. Работа с мастером функций и мастером диаграмм

 

В качестве примера рассмотрим процедуру построения графика функции y=cos²(px), при хÎ[0,1].

Для построения графика функции необходимо сначала построить таблицу ее значений (протабулировать) при различных значениях аргумента, причем обычно аргумент из­меняется с фиксированным шагом. Шаг выбирают таким, чтобы таб­лица значений функции отражала ее поведение на интервале табуляции.

В нашем случае будем считать, что шаг изменения аргумента равен 0,1. Не­обходимо найти: y(0), y(0,1), у(0,2), •••, y(1). С этой целью в диапазон ячеек А1:А11 введем следующие значения переменной

х: 0, 0.1, 0.2,..., 1. Отметим, что выбранные нами значения переменной образуют арифметическую прогрессию. Заполнение ячеек членами арифметической прогрессии в Excel можно осуществить двумя способами:

Первый способ. В ячейки А1 и А2 вводим первый и второй члены арифме­тической прогрессии и выделяем эти ячейки. После этого устанавливаем указатель мыши на маркере заполнения выделенного диапазона (маленький черный квадратик в правом нижнем углу) и протаскиваем его вниз до тех пор, пока не получится числовой ряд нужной длины.

Второй способ. В ячейку А1 вводим первый член арифметической прогрес­сии. Выбираем команду Правка, Заполнить, Прогрессия и в открывшемся диалоговом окне Прогрессия в группе Распо­ложение устанавливаем переключатель в положение По столбцам, а в группе Тип — в положение Арифметическая. В поле Шаг вводим значение 0.1, а в поле Предельное значение — 1. После нажатия кнопки ОК будет выполнено построение прогрессии.

С помощью команды Правка, Заполнить, Прогрессия мож­но создавать также геометрические прогрессии.

Вернемся к нашему примеру построения графика. В ячейку В1 введем формулу:

=СОS(ПИ()*А1)^2

Ввод формул в ячейку можно производить с клавиатуры или с помощью диалогового окна Мастер функций, вызываемого командой Вставка, Функция или нажатием кнопки f_x панели инст­рументов Стандартная. Мастер функций содержит список всех встроенных в Excel функций, а также справки по синтаксису функций и примеры их применения.

 

Рассмотрим приемы работы с мастером функций на примере ввода выше­упомянутой формулы. Выделим ячейку В1 и нажмем кнопку f_x панели ин­струментов Стандартная.

Это окно содержит два списка:

Категория - список, включающий одиннадцать категорий функций,

и Функция - список имен функций, входящих в выбранную категорию. Категория

Полный алфа­витный перечень содержит все встроенные функции Excel, имена кото­рых упорядочены в алфавитном порядке.

Категория 10 недавно использо­вавшихся содержит имена десяти недавно исполь­зовавшихся функций. Она ускоряет вызов функций, постоянно используе­мых пользователем.

Функция косинус относится к категории Математические. Выберем эту функцию и нажмем кнопку Далее. На экране появится второе диалоговое окно Мастера функций.

В поле число второго диалогового окна Мастера функций вводится аргумент функции. В рассматриваемом примере это пи () *А1. Конечно, его можно ввести с клавиатуры. Однако этот аргумент содержит встроенную функцию пи (), поэтому лучше, нажав кнопку Выбор имени функции, расположен­ную в Строке формул,найти функцию пи () в категории Математические. Так как функция пи () не имеет аргументов, то чтобы вернуться в диалоговое окно функции cos, укажите мышью на уже набранное имя функции cos в строке формул и щелкните левой кнопкой мыши.

В поле число с помощью клавиатуры вве­дем * и, щелкнув ячейку А1 рабочего листа, введем a1. Конечно, ссылку на ячейку можно ввести также с помощью клавиатуры, однако, такой способ ввода (щелчком на соответствующей ячейке) дает до­полнительную проверку правильности ввода. После нажатия кнопки Готово в ячейку В1 будет введена формула:

=COS(ПИ()*А1)

Теперь с помощью клавиатуры добавим в эту формулу операцию возведения в квадрат. После всех описанных действий в ячейку В1 будет введена формула:

=COS(ПИ()*А1) ^2

Для того чтобы завершить процесс табулирования функции, выделим ячейку В1, установим указатель мыши на маркере заполнения этой ячейки и протащим его вниз до ячейки В11.

 

Для построения графика функ­ции выделим диапазон ячеек В1:В11, содержащий таблицу значений функ­ции и вызовем Мастер диаграмм. Вызов мастера диаграмм производится либо с помощью команды Вставка, Диаграмма, На этом листе, либо нажатием кнопки панели инст­рументов Стандартная.

На первом шаге мастера диаграмм выбираем вид диаграммы, например,график.

На следующем шаге мастера диаграмм заполняем диалоговое окно следую­щим образом:

В группе Ряды данных находятся устанавлива­ем переключатель в положение В столбцах.

На вкладке Ряд в группе Подписи по оси Х укажем А1:А11.

Все данные заполнены – нажмите кнопку Готово.

2.2 Построение графика функции с одним условием

Рассмотрим пример построения графика функции

у=

при хÎ [0, 1].

 

Этот график строится так же, как в разделе 1, за одним исключением — в ячейку В1 вводится формула:

=ЕСЛИ(А1<0.5;(1+ABS(0.2-A1))/(l+Al+Al^2);A1^(1/3)).

Синтаксис логической функции если (if):

ЕСЛИ (лог выражение; значение_если_истина; значение_если_ложь).

Функция если возвращает значение_если_истина, если лог_выражение имеет значение ИСТИНА (TRUE), и значение_если_ложь — если лог_выражение имеет значение ложь (false).

Функция если используется для проверки значений формул и организации переходов в зависимости от результатов этой проверки.

2.3 Построение графика функции с двумя условиями

Рассмотрим пример построения графика

при хÎ[0,1].

График строится так же, как в разделе 1, только в ячейку В1 вводится формула:

=EСЛИ(A1<0.2;1+LN(1+A1); ЕСЛИ (A1<=0.8;(1+А1^(1/2))/(1+А1);2*ЕХР(-2*А1)))

2.4 Построение двух графиков в одной системе координат

Рассмотрим пример построения в одной системе координат графиков сле­дующих двух функций

у = 2sin(x) и

z = 3cos(2x) — sin(x)

при хÎ[-3, 0].

В диапазон ячеек А2:А17 вводим значения переменной x: от -3 до 0 с шагом 0,2.

В ячейки В1 и С1 вводим у и z, соответственно. В ячейки В2 и С2 вводим формулы:

=2*SIN (A2)

=3*COS (2*A2)-SIN (A2)

Выделим диапазон В2:С2 и установим указатель мыши на маркере заполне­ния этого диапазона и протащим его вниз так, чтобы заполнить диапазон В2:С17.

Выделим диапазон ячеек В2:С17, в который внесена таблица зна­чений двух функций, и вызовем мастера диаграмм.

Для наглядно­сти, графики функций можно различать по типу линий. Как это делается?

График, внешний вид которого мы хотим изменить, выделяется и с помо­щью контекстного меню (доступ посредством правой кнопки мыши) вызывается диалоговое окно Формат рядов данных, которое позволяет изменять тип, толщину и цвет линии, а также тип, цвет и фон маркера.

2.5 Построение поверхности

Рассмотрим пример построения поверхности:

z=x²-y², при х, уÎ[-1, 1].

В диапазон ячеек B1:L1 введем последовательность значений:

-1, -0.8,..., l переменной х, а в диапазон ячеек А2:А12 - последовательность значений: -1, -0.8,..., 1 переменной у.

В ячейку В2 введем формулу:

=$A2^{^}2-B$1^{^}2

Далее выделим эту ячейку, установим указатель мыши на ее маркере заполнения и протащим его так, чтобы заполнить диапазон B2:L12.

Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой — абсолютную ссылку на строку с этим именем. Поэтому при протаскивании формулы из ячейки В2 в ячейки диапазона B2:L12 в них будет найдено значение z при соответствующих значениях х и у.

Итак, таблица значений функции z при различных значениях переменных создана.

Перейдем к построению поверхности.

Выделим диапазон ячеек A1:L12, со­держащий таблицу значений функции и ее аргументов, и вызовем Мастера диаграмм. Выбираем тип диаграммы — Поверхность. Дальнейшие шаги аналогичны тем, что описаны в разделе 1.

 

3 Нахождение корней уравнения

Рассмотрим пример отыскания всех корней уравнения:

х³ - 0,01х² - 0,7044х + 0,139104 =0.

Отметим, что у полинома третьей степени имеется не более трех веществен­ных корней. Для нахождения корней их предварительно нужно локализо­вать. С этой целью необходимо построить график функции или протабулировать ее.

Например, протабулируем наш полином на отрезке [-1, 1] с шагом 0,2. Для этого в ячейки А2:А11 введем значения х, в ячейку В2 вве­дем следующую формулу:

=A2^{^}3-0.01*A2^{^}2-0.7044*A2+0.139104.

Построим график функции, как указано в разделе 2.2.

Из графика видно, что полином меняет знак на интервалах: [-1, -0,8], [0,2, 0,4] и [0,6, 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Поскольку полином третьей степени имеет не более трех действительных корней, значит, мы локализовали все его корни.

Найдем корни полинома методом последовательных приближений с помо­щью команды Сервис, Подбор параметра. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открывае­мого командой Сервис, Параметры.

Зададим относительную погрешность и предельное число итераций, равными 0.0000l и 1000, соответственно. В качестве начальных значений приближе­ний к корням можно взять любые точки из отрезков локализации корней.

Возьмем, например, их средние точки: -0.9, 0.3 и 0.7 и введем их в диапа­зон ячеек С2:С4. В ячейку D2 введем формулу:

=С2^3-0.01*С2^2-0. 7044*С2+0.139104

Выделим эту ячейку и с помощью маркера заполнения протащим введенную в нее формулу на диапазон D2:D4.

Таким образом, в ячейках D2:D4 вычис­ляются значения полинома при значениях аргумента, введенного в ячейки С2:С4, соответственно.

Теперь выберем команду Сервис, Подбор параметра и за­полним диалоговое окно Подбора параметра.

В поле Установить в ячейке введем D2. Отметим, что в этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значе­ние левой части уравнения. Для нахождения корня уравнения с помощью средства подбора параметров надо записать уравнение так, чтобы его правая часть не содержала переменную.

В поле Значение вводим 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем C2 (в этом поле дается ссылка на ячейку, отведенную под переменную).

Вводить ссылки на ячейки в поля диалогового окна Подбор параметра удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в на­шем примере $D$2 и $C$2).

После нажатия кнопки ОК средство подбора параметров находит прибли­женное значение корня, которое помещает в ячейку С2. В данном случае оно равно -0. 919999.

Аналогично в ячейках СЗ и С4 находим два оставшихся корня. Они равны 0.20999 и 0.71999.

4 Ход работы

1. Изучить разделы 2 и 3 данных методических указаний

2. Выполнить все предлагающиеся примеры. Зафиксировать полученные результаты в отчете о выполнении лабораторной работы.

3. Выполнить представленные в разделе 5 задания самостоятельно. Зафиксировать полученные результаты в отчете о выполнении лабораторной работы.

4. Подготовить отчет, сформулировать выводы.

5. Варианты заданий к выполнению лабораторной работы

Вариант 1

(а) Построить в разных системах координат при хÎ[-2, 2] графики следующих функций:

 

(b) Построить в одной системе координат при хÎ[-2, 2] графики следующих двух функций:

у = 2sin(x)cos(x), z=3cos²(2x)sin(x)

(c) Построить поверхность z=x²-2y², при x,yÎ[-1,1].

(d) Найти все корни уравнения х³ - 2,92x²+1,4355х+0,791136 = 0.

Вариант 2

(а) Построить в разных системах координат при хÎ[-2, 2] графики следующих функций:

 

 

(b) Построить в одной системе координат при хÎ[-2, 2] графики следующих двух функций:

у = 2sin(px) - 3cos(px), z=cos²(2px) - 2sin(px)

(c) Построить поверхность z=3x² - 2sin²(y)y², при x,yÎ[-1,1].

(d) Найти все корни уравнения х³ - 2,56x²-1,325х+4,39506 = 0.