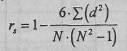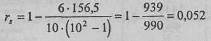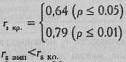Пример 1 - корреляция между двумя признаками

Висследовании, моделирующем деятельность авиадиспетчера (Одерышев Б.С., Шамова Е.П., Сидоренко Е.В., Ларченко Н.Н., 1978), группа испытуемых, студентов физического факультета ЛГУ проходила подготовку перед началом работы на тренажере. Испытуе­мые должны были решать задачи по выбору оптимального типа взлет­но-посадочной полосы для заданного типа самолета. Связано ли коли­чество ошибок, допущенных испытуемыми в тренировочной сессии, с показателями вербального и невербального интеллекта, измеренными по методике Д. Векслера?

Таблица 6.1

Показатели количества ошибок в тренировочной сессии и показатели уровня вербального и невербального интеллекта у студентов-физиков (N=10)

Испытуемый	Количество ошибок	Показатель вербального интеллекта	Показатель невербального интеллекта
	Т.А.
	П.А.
	Ч.И.
	Ц.А.
	См.А.			. 127
	К.Е.
	К.А.
	Б.Л.
	И.А.
	Ф.В.
Суммы
Средние	19,2	130,9	105,7

Сначала попробуем ответить на вопрос, связаны ли между собой показатели количества ошибок и вербального интеллекта.

Сформулируем гипотезы.

H₀: Корреляция между показателем количества ошибок в тренировочной сессии и уровнем вербального интеллекта не отличается от нуля.

H₁: Корреляция между показателем количества ошибок в тренировочной сессии и уровнем вербального интеллекта статистически значимо отличается от нуля.

Далее нам необходимо проранжировать оба показателя, Приписы­вая меньшему значению меньший ранг, затем подсчитать разности меж­ду рангами, которые получил каждый испытуемый по двум переменным (признакам), и возвести эти разности в квадрат. Произведем все необ­ходимые расчеты в таблице.

В Табл. 6.2 в первой колонке слева представлены значения по показателю количества ошибок; в следующей колонке - их ранги. В третьей колонке слева представлены значения по показателю вербаль­ного интеллекта; в следующем столбце - их ранги. В пятом слева пред­ставлены разности d между рангом по переменной А (количество оши­бок) и переменной Б (вербальный интеллект). В последнем столбце представлены квадраты разностей - d².

Таблица 6.2

Расчет d² для рангового коэффициента корреляции Спирмена r_s при сопоставлении показателей количества ошибок и вербального интеллекта у студентов-физиков (N=10)

Испытуемый

Переменная А количество ошибок

Переменная Б вербальный интеллект.

d (ранг А - - ранг Б)

J2

Индивидуальные значения

Ранг

Индивидуальные значения

Ранг

ТА.

2

ПА.

5.5

4,5

20.25

Ч.И.

Ц.А.

-1

См.А.

-4

К.Е.

К.А.

-4

Б.Л.

-2

И.А.

5,5

-4,5

20,25

Ф.В.

Суммы

156,5

Коэффициент ранговой корреляции Спирмена подсчитывается по формуле:

где d - разность между рангами по двум переменным для каж­дого испытуемого;

N - количество ранжируемых значений, в. данном случае ко­личество испытуемых.

Рассчитаем эмпирическое значение r_s:

Полученное эмпирическое значение г_s близко к 0. И все же определим критические значения r_s при N=10 по Табл. XVI Приложения 1:

Ответ: H₀ принимается. Корреляция между показателем коли­чества ошибок в тренировочной сессии и уровнем вербального интел­лекта не отличается от нуля.

Теперь попробуем ответить на вопрос, связаны ли между собой показатели количества ошибок и невербального интеллекта.

Сформулируем гипотезы.

H₀: Корреляция между показателем количества ошибок в тренировочной сессии и уровнем невербального интеллекта не отличается от 0.

H₁: Корреляция между показателем количества ошибок в тренировочной сессии и уровнем невербального интеллекта статистически значимо отличается от 0.

Результаты ранжирования и сопоставления рангов представлены в Табл. 6.3.

Таблица 6.3

Расчет d² для рангового коэффициента корреляции Спирмена r_s при сопоставлении показателей количества ошибок и невербального интеллекта у студентов-физиков (N=10)

Испытуемый	Переменная А количество ошибок	Переменная Е ; невербальный интеллект	d (ранг А — — ранг Б)	d2
Индивидуальные	Ранг	Индивидуальные	Ранг
значения		значения
	Т.А.
	П:А.
	Ч.И.
	Ц-А. „					-7
	См.А.					-5
	К.Е.
	К.А.					-2
	Б.Л.
	И.А.					-7
	Ф.В.
Суммы

Мы помним, что для определения значимости r_s неважно, являет­ся ли он положительным или отрицательным, важна лишь его абсолют­ная величина. В данном случае:

r_{s эмп}<r_{s ко}.

Ответ: H₀ принимается. Корреляция между показателем коли­чества ошибок в тренировочной сессии и уровнем невербального интел­лекта случайна, r_s не отличается от 0.

Вместе с тем, мы можем обратить внимание на определенную тенденцию отрицательной связи между этими двумя переменными. Возможно, мы смогли бы ее подтвердить на статистически значимом уровне, если бы увеличили объем выборки.