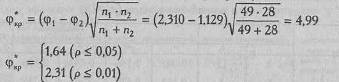Решение задачи 11

Поскольку сравниваются две выборки, выбираем критерий φ * Фишера. Однако "на глаз" трудно решить, какая команда врачей должна считаться большей по составу, а какая - меньшей. Нам необходимо найти точку, в которой накапливаются максимальные различия между двумя распределениями, для того, чтобы применение критерия φ * было максимально эффективным. Для этого вначале используем алгоритм опре­деления максимальной разности между накопленными частостями, ис­пользуемый в критерии λКолмогорова-Смирнова (Алгоритм 15).

Результаты применения алгоритма представлены в Табл. 9.23

Таблица 9.23

Выявление точки максимальной разности между эмпирическими рас­пределениями "количества партнеров у врачей с фондами (n ₁=49) и врачей без фондов (n ₂⁼28)

 

количество партнеров	Эмпирические частоты	Эмпирические частости	Накопленные эмпирические частости	Разность
f1	f2	f * 1	f * 2	∑f * 1	∑f * 2	(∑f * 1 - ∑f * 2)
	2 и менее партнеров			0,041	0,536	0,041	0,536	0,495
	3-4 партнера 5-6 партнеров			0,122   0,551	0,179   0,286	0,163   0,714	0,715   1,000	0,286
	7 и более партнеров			0,286		1,000	1,000
Суммы			1,000	1,000

Как видно из Табл. 9.23, максимальная разность накопленных частостей падает на 2-й разряд (3-4 партнера). Поскольку вопрос в задаче касается предположения о том, что в приемных с фондами рабо­тают большие по составу команды врачей, чем в приемных без фондов, будем считать, что если партнеров более 4-х, то "эффект есть", а если партнеров 4 и менее, то "эффекта нет". Построим соответствующую четырехклеточную таблицу и определим % доли "эффекта" в каждой из двух выборок.

Таблица 9.24

Четырехклеточная таблица для подсчета критерия φ * при сопоставле­нии выборок врачей с фондами (n ₁=49) и врачей без фондов (п ₂ =28) по признаку количества партнеров

Группы	"Есть эффект" более 4 партнеров	"Нет эффекта" не более 4 партнеров	Суммы
1 группа -врачи с фондами		(83,7%)		(16,3%)
2 группа -врачи без фондов		(28,6%)		(71,4%)
Суммы

 

Сформулируем гипотезы.

H₀: Доля лиц, имеющих более 4-х партнеров, в выборке врачей с фон­дами не больше, чем в выборке врачей без фондов.

H₁: Доля лиц, имеющих более 4-х партнеров, в выборке врачей с фон­дами больше, чем в выборке врачей без фондов. По Табл. XII Приложения 1 определяем углы φ:

φ _1(83,7%)=2,310

φ _2(28,6%)=1,129

Рассчитаем эмпирическое значение критерия φ *:

По Табл. XIII Приложения 1 определяем, какому уровню значи­мости соответствует эта величина φ *: р <0,001.

φ* _эмп > φ* _кр (p <0,001)

Ответ: H₀ отклоняется. Принимается H₁. Доля лиц, имеющих более 4-х партнеров, в выборке врачей с фондами больше, чем в вы­борке врачей без фондов (р <0,001).

Фирма с высокой степенью уверенности может ориентироваться на эту тенденцию в построении своей стратегии продвижении товара. Но то, как она будет ее учитывать, уже выходит за рамки данной ста­тистической задачи.

Решение задачи 12

Обследована одна выборка испытуемых, поэтому останавливаем выбор на биномиальном критерии т. В параграфе 4.2, посвященному методу χ², эта задача предположительно должна была решаться с помощью критерия χ². Однако, поскольку количество наблюдений n <300, а вероятность выбора каждой из дорожек при равновероятном выборе составляет ½, т.е. P=Q=0,50, мы можем воспользоваться биномиальным критерием, кото­рый несравненно проще в использовании, чем критерий χ². Воспроизведем таблицу частот.

Таблица 9.25

Эмпирические частоты выбора правой и левой симметричных дорожек (n =70)

Выбрана правая дорожка	Выбрана левая дорожка	Суммы

Сформулируем гипотезы.

H₀: Частота выбора правой дорожки не превышает частоты, которая соответствует вероятности случайного выбора.

H₁: Частота выбора правой дорожки превышает частоту, которая соот­ветствует вероятности случайного выбора.

Определим теоретическую частоту выбора одной из дорожек при случайном выборе:

f _теор= n · р =70·0,50=35

Поскольку f _эмп > f _теор, используем биномиальный критерий m, a не его "зеркальное отражение" (критерий знаков G).

По Табл. XIV Приложения 1 определяем критические значения m для n =70:

Ответ: H₀ отклоняется. Принимается H₁. Частота предпочтения правой дорожки превышает частоту, которая соответствует вероятности случайного выбора (р <0,01).

Наблюдатель может обоснованно утверждать, что из данных двух симметричных дорожек чаще выбирается правая. Чем это объясняется— уже другой вопрос, выходящий за рамки задачи (см. п. 4.2).