Упражнения для самостоятельного решения
1. Найти  .
a. 6
b. -6
c. -18
d. -24
| 2. Найти  .
a. 6
b. 14
c. -6
d. -4
| 3. Найти  .
a. -24
b. 8
c. 24
d. -8
| 4. Найти  .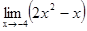
a. 20
b. 28
c. 36
d. -4
| 5. Найти  .
a. -36
b. 21
c. -21
d. -33
| 6. Найти  .
a. -12
b. 4
c. 12
d. -4
| 7. Найти  .
a. 4
b. -4
c. -5
d. -6
| 8. Найти  .
a. -10
b. -6
c. 6
d. 10
|
1. Выберите определение непрерывности функции в точке
a. Функция является непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции
b. Функция является непрерывной в точке, если существует конечный предел функции в этой точке
c. Точка является точкой непрерывности функции, если эта функция определена в некоторой окрестности этой точки
d. Функция у называется непрерывной в точке х, если 
| 2. Выберите определение непрерывности функции в точке
a. Функция является непрерывной в точке а, если 
b. Функция у называется непрерывной в точке х, если
c. Функция является непрерывной в точке, если существует конечный предел функции в этой точке, который равен значению функции в этой точке
d. Точка является точкой непрерывности функции, если эта функция определена в некоторой окрестности этой точки
| 3. Выберите определение непрерывности функции в точке
a. Функция является непрерывной в точке, если существует конечный предел функции в этой точке
b. Функция является непрерывной в точке а, если
c. Функция у называется непрерывной в точке, если 
d. Точка является точкой непрерывности функции, если эта функция определена в некоторой окрестности этой точки
| 4. Выберите определение непрерывности функции в точке
a. Функция является непрерывной в точке, если существует конечный предел функции в этой точке
b. Функция у называется непрерывной в точке, если
c. Функция является непрерывной в точке а, если
d. Функция у называется непрерывной в точке а, если 
|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Весы настольные циферблатные Весы настольные циферблатные РН-10Ц13 (рис.3.1) выпускаются с наибольшими пределами взвешивания 2...
Хронометражно-табличная методика определения суточного расхода энергии студента Цель: познакомиться с хронометражно-табличным методом определения суточного расхода энергии...
ОЧАГОВЫЕ ТЕНИ В ЛЕГКОМ Очаговыми легочными инфильтратами проявляют себя различные по этиологии заболевания, в основе которых лежит бронхо-нодулярный процесс, который при рентгенологическом исследовании дает очагового характера тень, размерами не более 1 см в диаметре...
|
Реформы П.А.Столыпина Сегодня уже никто не сомневается в том, что экономическая политика П...
Виды нарушений опорно-двигательного аппарата у детей В общеупотребительном значении нарушение опорно-двигательного аппарата (ОДА) идентифицируется с нарушениями двигательных функций и определенными органическими поражениями (дефектами)...
Особенности массовой коммуникации Развитие средств связи и информации привело к возникновению явления массовой коммуникации...
|
|
