Задания к контрольной работе №3.
Задачи 310-319. Исследовать сходимость числового ряда.
310. a) 311. a) 312. a) 313. a) 314. a) 315. a) 316. a) 317. a) 318. a) 319. a)
Задачи 320-329. Найти интервал сходимости степенного ряда.
320. a) 321. a) 322. a) 323. a) 324. a) 325. a) 326. a) 327. a) 328. a) 329. a)
Задачи 330-339. Вычислить приближенное значение функции f(х) в заданной точке, разложив ее в степенной ряд с точностью до четырех значимых слагаемых. Указать точность оценки.
330. 332. 334. 336. 338.
Задачи 340-349. Вычислить приближенное значение определенного интеграла
340. 342. 344. 346. 348.
Задачи 350-359. Разложить данную функцию ¦(х) в ряд Фурье в интервале (а; в):
350. ¦(х) = 2х + 1 в интервале (-1,1)
351. ¦(х) = х + 4 в интервале (-2p,2p)
352. ¦(х) = х - 1 в интервале (0,2p)
353. ¦(х) = 3 + х в интервале (-2p,2p)
354. ¦(х) = -4 - 5х в интервале (-1,1)
355. ¦(х) = 1 - 2х в интервале (-2,2)
356. ¦(х) = х + 6 в интервале (-2p,2p)
357. ¦(х) = х - 3 в интервале (0,2p)
358. ¦(х) = 3 - 4х в интервале (-2,2)
359. ¦(х) = 2х + 3 в интервале (-2p,2p)
Контрольная работа №5 (2 курс 1 семестр) «Дифференциальные уравнения» Тематический план
1. Дифференциальное уравнение и его порядок. Задача Коши. Общее и частное решение, общий и частный интеграл. 2. Дифференциальные уравнения с разделяющимися переменными. 3. Однородные дифференциальные уравнения первого порядка. 4. Линейные дифференциальные уравнения первого порядка. 5. Интегрирование некоторых дифференциальных уравнений второго порядка путем понижения порядка уравнения. 6. Структура общего решения линейного дифференциального уравнения второго порядка без правой части. 7. Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами и без правой части. Характеристическое уравнение. 8. Структура общего решения линейного дифференциального уравнения с правой частью. 9. Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью специального вида. 10. Отыскание частного решения линейного дифференциального уравнения с постоянными коэффициентами и с правой частью специального вида. 11. Преобразование Лапласа. 12. Свойства преобразования Лапласа. 13. Изображения простейших оригиналов. 14. Основные теоремы операционного исчисления. 15. Изображение производных. 16. Теорема разложения в операционном исчислении. 17. Интегрирование дифференциальных уравнений операторным методом.
|

 b)
b) 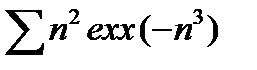
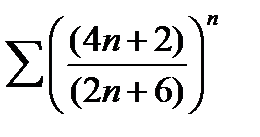 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 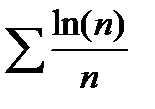
 b)
b) 
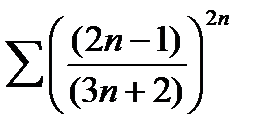 b)
b) 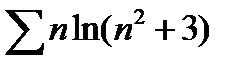
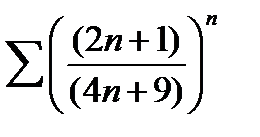 b)
b) 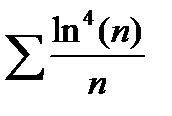
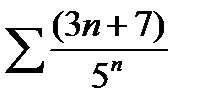 b)
b) 
 b)
b) 
 b)
b) 
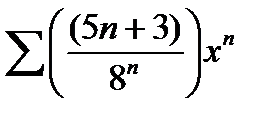 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 

 331.
331. 


 333.
333. 


 335.
335. 


 337.
337. 


 339.
339. 

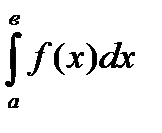 разложив подинтегральную функцию в степенной ряд с точностью до четырех значимых слагаемых и затем проинтегрировав его.
разложив подинтегральную функцию в степенной ряд с точностью до четырех значимых слагаемых и затем проинтегрировав его. 341.
341. 
 343.
343. 
 345.
345. 
 347.
347. 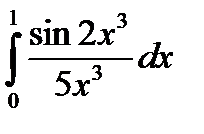
 349.
349. 



