Задания к контрольной работе №1.
Задачи 110-119. Вычислить определитель матрицы третьего порядка: a) методом треугольников; b) разложением по первой строке.
110. а)
111. а)
112. а)
113. а)
114. а)
115. а)
116. а)
117. а)
118. а)
119. а)
Задачи 120-129. Решить системы линейных уравнений. Задача a) решается методом Крамера; b) методом Гаусса.
Х1 + Х2 - Х3 = 1 2Х1 + Х2 - 3Х3 = 2 120. a) Х1 - 2Х2 + 2Х3 = 1 b) Х1 - Х2 + 2Х3 = 3 2Х1 + 2Х2 - 3Х3 = 1 Х1 + 2Х2 - Х3 = 3
2Х1 + Х2 + Х3 = 6 3Х1 + Х2 - 3Х3 = -2 121. a) Х1 - Х2 + 2Х3 = 0 b) -Х1 + 2Х2 + Х3 = 3 Х1 + 2Х2 - 3Х3 = 2 2Х1 + 3Х2 - Х3 = 3
2Х1 + 3Х2 - Х3 = 2 -Х1 + 2Х2 - Х3 = -2 122. a) -Х1 + 2Х2 + Х3 = 4 b) 2Х1 - Х2 + Х3 = 6 2Х1 - 3Х2 + Х3 = 2 Х1 + Х2 - 3Х3 = 1
-Х1 + 2Х2 + 3Х3 = 3 -3Х1 + 3Х2 + 5Х3 = -1 123. a) 2Х1 + 3Х2 - 4Х3 = 3 b) 2Х1 - Х2 + 3Х3 = 6 3Х1 - 4Х2 + 2Х3 = 4 -2Х1 + 2Х2 - Х3 = -5
2Х1 + 3Х2 - Х3 = 2 -2Х1 + Х2 - Х3 = -2 124. a) Х1 - 2Х2 + Х3 = 2 b) Х1 - Х2 - Х3 = -1 -Х1 + Х2 + Х3 = 3 -Х1 + 2Х2 + Х3 = 2
3Х1 - Х2 + 4Х3 = 2 2Х1 + Х2 -Х3 = 4 125. a) Х1 + Х2 + Х3 = 2 b) -Х1 + 3Х2 + Х3 = 2 2Х1 - Х2 + Х3 = 1 Х1 + 2Х2 - Х3 = 3
3Х1 + Х2 - 2Х3 = 1 2Х1 + Х2 - Х3 = 1 126. a) -Х1 + 2Х2 + 3Х3 = 2 b) -Х1 + 2Х2 + Х3 = 3 Х1 + Х2 - 3Х3 = 3 Х1 + 3Х2 - Х3 = 2
3Х1 - 2Х2 + 3Х3 = -2 -2Х1 + 4Х2 - Х3 = 1 127. a) -Х1 + 3Х2 - Х3 = 3 b) Х1 + 2Х2 + Х3 = 4 2Х1 - 2Х2 + Х3 = -3 -2Х1 - Х2 + Х3 = -2
3Х1 - 2Х2 + 3Х3 = 1 -Х1 + 2Х2 - Х3 = 2 128. a) 2Х1 + Х2 - 4Х3 = 3 b) Х1 - Х2 + 2Х3 = 1 -Х1 + 3Х2 - 2Х3 =2 Х1 + 2Х2 - Х3 = 4
2Х1 + Х2 + Х3 = 2 Х1 + 2Х2 - 3Х3 = -1 129. a) -Х1 + Х2 + Х3 = -1 b) 2Х1 - 3Х2 + Х3 = 5 Х1 + 3Х2 - Х3 = -3 2Х1 + 4Х2 - 2Х3 = -2
Задачи 130-139. Даны координаты вершин пирамиды А1А2А3А4. Найти: 1) длину ребра А1А2 и ребра А1А4; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды А1А2А3А4; 6) уравнение прямой, проходящей через точки А1А2; 7) уравнение плоскости точек А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3; 9) найти расстояние от плоскости грани А1А2А3 до т. А4; 10) найти расстояние от плоскости грани А1А2А3 до начала координат.
Номера вариантов: 130. А1(3; 2; 5), А2(2; 1; 2), А3(3; 2; 1), А4(3; 5; 0). 131. А1(-2; 4; 0), А2(4; 0; -2), А3(3; 6; 4), А4(6; 6; 4). 132. А1(-4; 6; 5), А2(6; 3; 4), А3(2; 0; -5), А4(3; 5; 6). 133. А1(2; 6; -4), А2(4; 5; 4), А3(5; -2; 4), А4(4; 5; 4). 134. А1(8; -6; 4), А2(-2; 6; 2), А3(6; 8; 1), А4(7; 1; 3). 135. А1(4; 8; 2), А2(5; 2; 4), А3(5; -7; 4), А4(4; 1; 9). 136. А1(5; 6; -5), А2(4; 3; 5), А3(4; 6; 1), А4(6; -8; 3). 137. А1(-3; 2; 3), А2(5; -7; 4), А3(4; 3; 1), А4(-2; 3; 7). 138. А1(-5; 4; -4), А2(1; 6; 5), А3(5; 6; -6), А4(-8; 10; 7). 139. А1(7; -5; 3), А2(-6; 4; 8), А3(3; 5; 7), А4(-9; 4; 1). Контрольная работа №3 (1 курс 2 семестр) «Ряды» Тематический план.
1. Числовой ряд и его сходимость. 2. Необходимое условие сходимости числового ряда. 3. Геометрический ряд. Гармонический ряд. 4. Ряды с положительными членами. Сравнение рядов. 5. Призрак Даламбера. Корневой признак Коши. 6. Интегральный признак сходимости ряда. 7. Признак Лейбница сходимости знакочередующегося ряда. 8. Ряды с членами любого знака. Абсолютная сходимость. 9. Свойства абсолютно сходящихся рядов. 10. Функциональный ряд. Область сходимости. 11. Степенной ряд. Теорема Абеля, радиус сходимости. 12. Интегрирование и дифференцирование степенных рядов. 13. Ряд Тейлора. Коэффициенты ряда Тейлора. 14. Разложение показательной и тригонометрических функций в ряд Тейлора. Формула Эйлера для показательной функции от мнимого аргумента. 15. Биномиальный ряд. Разложение логарифма в степенной ряд. 16. Тригонометрический ряд. Ряд Фурье. Коэффициенты ряда Фурье. 17. Неполные ряды Фурье. Свойства неполного ряда Фурье 18. Ряд Фурье в комплексной форме. 19. Преобразование Фурье. Понятие об интегральных преобразованиях.
|

 b)
b) 
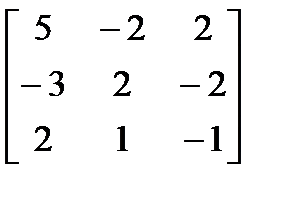 b)
b) 
 b)
b) 
 b)
b) 
 b)
b) 
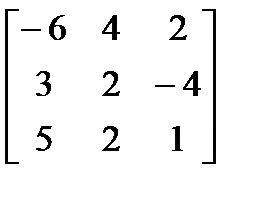 b)
b) 
 b)
b) 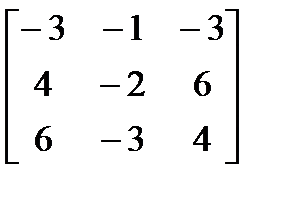
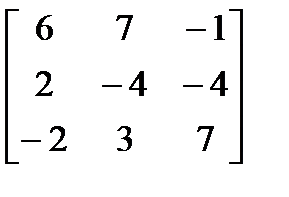 b)
b) 
 b)
b) 
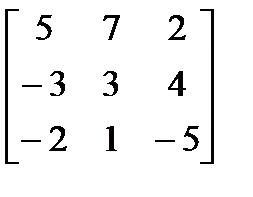 b)
b) 



