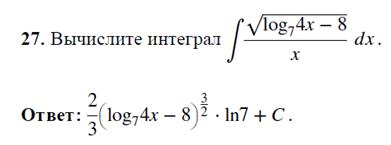Интегрирование рациональных функций.
Условные экстремумы Метод исключения переменной
Метод множителей Лагранжа
Наибольшее и наименьшее значения дифференцируемой функции на замкнутом ограниченном множестве.
Как найти. Вычислить значение функции в точках (кандидатах): 1) стационарные точки в данной области (см. локальные экстремумы); 2) точки на границе: Ø в случае многоугольника - угловые точки и стационарные на сторонах; Ø в случае криволинейной области – стационарные точки функции Лагранжа. На границе: метод исключения переменной
На границе: метод множителей Лагранжа
Линейные дифференциальные уравнения первого порядка. Метод Бернулли.
Уравнение Бернулли.
Если α; >0, тогда у=0 – стационарное решение, Если α<0, то стационарного решения нет.
Линейные дифференциальные уравнения первого порядка с постоянными коэффициентами
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Решить ЛОДУ 2-го порядка:
Метод интегрирования по частям
Пример 1. 1. Ответ: 2. 3. 4.
5.
Интегрирование рациональных функций
Если дробь не является правильной, т.е. степень числителя не меньше степени знаменателя, можно выполнить деление с остатком и представить выражение в виде суммы многочлена и правильной дроби. Поэтому будем предполагать дробь несократимой и правильной (n < m). Известно, что любая правильная дробь может быть представлена в виде суммы простейших дробей вида:
где k > 1;
где n > 1, а p 2 – 4 q < 0; где величины A, B, … можно найти методом неопределенных коэффициентов. Поясним этот метод на примерах. Пример 2. Вычислить
Пример 3. Вычислить
Пример 4. Вычислить
|
~ 
- характеристическое уравнение
, λ1 и λ2 
R
, λ1 = λ 2 = λ
, 
. Ответ: 
. Ответ: 
. Ответ: 
,
,
.
.
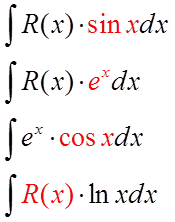
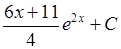
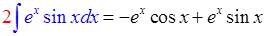
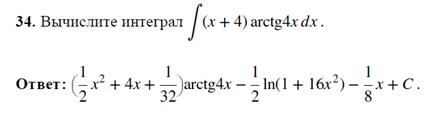
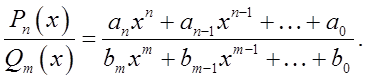
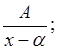
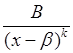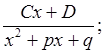
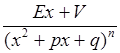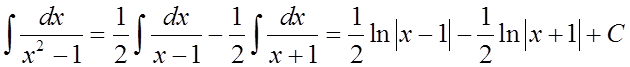
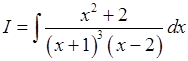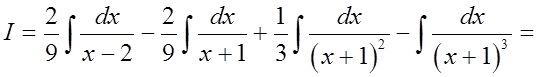
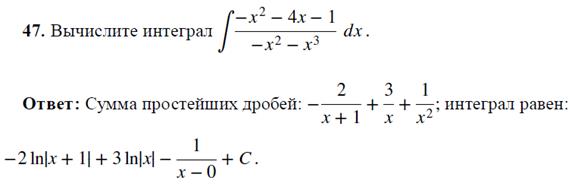
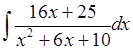