Теория метода и описание установки.
Удельной теплоемкостью С газа называется скалярная физическая величина, численно равная количеству теплоты Q, которое необходимо сообщить единице массы газа, чтобы увеличить его температуру на 1 К:
Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись первым законом термодинамики, который гласит: количество теплоты Q, сообщенное системе, затрачивается на увеличение ее внутренней энергии
При изохорическом (V=const) нагревании газа
Из формулы (1) следует, что
При изобарном (Р=const) нагревании газа тепло, сообщаемое газу идет и на увеличение внутренней энергии и на совершение газом работы против внешних сил:
поэтому Сравнивая уравнения (3) и (4), получаем Отношение удельных теплоемкостей при постоянном давлении и при постоянном объеме
В данной работе прелагается один из самых простых методов определения метод Клемана и Дезорма. Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой, т.е. считается, что процесс передачи тепла системе от окружающей среды отсутствует. Экспериментальная установка состоит из стеклянного баллона А (рис. 1), соединенного с манометром В и с насосом.
Рис. 1
Если про помощи насоса накачать в баллон некоторое количество воздуха, то давление и температура воздуха внутри баллона повысятся. Вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха, находящегося в баллоне, сравнятся с температурой внешней среды Давление, установившееся в баллоне
где Р - атмосферное давление; Н - разность уровней жидкости в манометре; В - коэффициент перехода от разности уровней к давлению. Таким образом, состояние воздуха внутри баллона, которое назовем 1 состоянием, характеризуется параметрами
Если на короткое время открыть кран С, то воздух в баллоне будет расширяться. Этот процесс расширения можно считать адиабатическим. Давление в баллоне установится равным атмосферному Р, температура газа понизится до Следовательно, в конце адиабатического процесса, что назовем 2 состоянием, параметры состояния газа будут Р; Применяя к 1 и 2 состояниям уравнение (5), получим:
Охладившийся при адиабатическом расширении воздух в баллоне через некоторое время вследствие теплообмена нагреется до температуры внешней среды
где h- новая разность уровней в манометре. Объем воздуха не изменится и будет равен Это состояние воздуха, которое назовем 3 состоянием, характеризуется параметрами
Так как в состояниях 1 и 3 воздух имеет одну и ту же температуру (P+вH)
Возведем обе части уравнения в степень
Решая совместно уравнения (6) и (7), получим:
Логарифмируя это выражение и решая относительно
Так как давления Р, Р+вН и Р+вh мало отличаются друг от друга, то разности логарифмов можно принять пропорциональными разностям самих давлений и приближенно положить
|

 (1)
(1) и на работу А, совершаемую системой против внешних сил
и на работу А, совершаемую системой против внешних сил (2)
(2)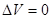 , следовательно, и А=0. Тогда все подводимое к газу тепло идет на увеличении его внутренней энергии:
, следовательно, и А=0. Тогда все подводимое к газу тепло идет на увеличении его внутренней энергии: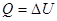
 (3)
(3)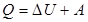 ,
, (4)
(4) .
. играет в термодинамике весьма важную роль. В частности оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа
играет в термодинамике весьма важную роль. В частности оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа (5)
(5) -
-
 .
.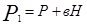 ,
, ;
; 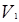 и
и 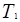
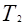 , а объем будет равен
, а объем будет равен 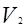 .
.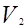 ,
,  или
или  (6).
(6).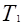 , давление возрастет до некоторой величины
, давление возрастет до некоторой величины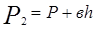 ,
, .
. ;
;  ;
; 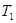
 (P+вh)
(P+вh) 
 :
:  (7)
(7)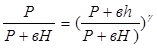


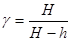 (8)
(8)
 Таким образом, экспериментальное определение
Таким образом, экспериментальное определение  сводится к измерению H и h, то есть формула (8) является расчетной формулой для определения коэффициента
сводится к измерению H и h, то есть формула (8) является расчетной формулой для определения коэффициента 


