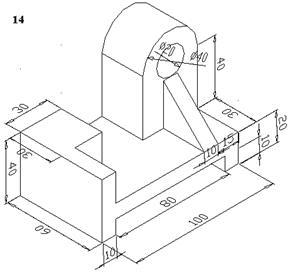
Отыскание точки пересечения прямой линии с прямой пирамидой и с прямым круговым конусом с помощью средств AutoCAD

 

Цель: найти точку пересечения прямой линии с пирамидой с помощью проецирующей вспомогательной плоскости.

 

Контрольные вопросы:

 

1. Какой должна быть вспомогательная секущая плоскость, используемая при решении поставленной задачи, что бы облегчить решение задачи?

2. Сформулируйте общий принцип решения задачи пересечения поверхностей с прямой линией.

Задание 1: найти точки пересечения прямой а с прямой семигранной пирамидой; объекты заданы проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении Д).

 

Решим задачу с помощью вспомогательной секущей плоскости Ф, которую проведем через прямую а. Решение задачи упрощается, если плоскость будет проецирующей. Применим фронтально-проецирующую плоскость, совместим ее фронтальный след с фронтальной проекцией прямой a (рис. 8.1). Найдем горизонтальную проекцию сечения пирамиды этой плоскостью, сделаем это так же, как в лабораторной работе № 5 (рис. 8.2).

Рисунок 8.1 – Проекции пирамиды и прямой общего положения	Рисунок 8.2 – Горизонтальная проекция сечения

 

Найдем горизонтальные, а затем, по соответствию, фронтальные проекции точек пересечения прямой с сечением, это и будут точки пересечения прямой и пирамиды (рис. 8.3). Трехмерная модель отыскания точек пересечения приведена на рисунке 8.4.

Рисунок 8.3 – Проекции точек пересечения прямой и пирамиды

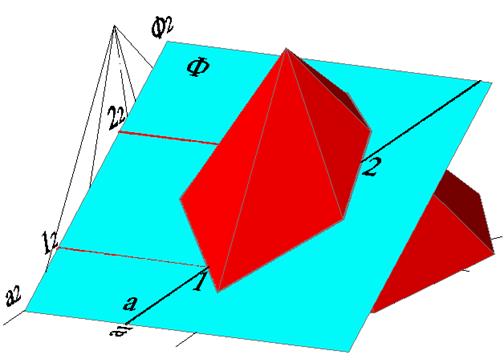
Рисунок 8.4 – Трехмерная модель отыскания точек пересечения

Задание 2: найти точки пересечения прямой линии с прямым круговым конусом; объекты заданы проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении Д).

 

Исходные данные приведены на рисунке 8.5. Для решения задачи применим вспомогательную секущую плоскость, которую проведем через вершину конуса и две точки на прямой. Такая плоскость пересекает конус по образующим, заданная прямая лежит в плоскости. Зададим две точки на прямой a (рис. 8.6).

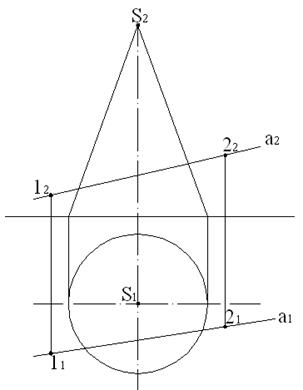
Рисунок 8.5 – Проекции конуса и прямая a	Рисунок 8.6 – Задание точек на прямой

 

Построим секущую плоскость:

- при помощи команды LINE, проведем две прямые через вершину конуса и точки 1₂ и 2₂; эти две прямые определяют фронтальную проекцию секущей плоскости, таким же образом построим горизонтальные проекции этих прямых (рис. 8.7);

- с помощью команды EXTEND найдем фронтальные проекции точек пересечения прямых S1 и S2 с плоскостью основания конуса – М₂ и N₂ (рис. 8.8);

- найдем горизонтальные проекции этих точек, это удобно с помощью команды FILLET, которая может быть применена для продления отрезков до точки пересечения (рис. 8.9).

Прямая M₁N₁ – след секущей плоскости на плоскости основания конуса, построив ее можно найти точки пересечения следа плоскости с основанием конуса – А₁ и В₁ (рис. 8.10).

Рисунок 8.7 – Построение прямых S1 и S2	Рисунок 8.8 – Отыскание точек М2 и N2

Рисунок 8.9 – Отыскание точек М1 и N1	Рисунок 8.10 – Построение отрезка M1N1

Теперь можно построить горизонтальные проекции образующих, являющихся сечением конуса плоскостью 1S2 – A₁S₁ и B₁S₁ (рис 8.11).

Эти образующие и исходная прямая лежат в секущей плоскости, поэтому, точки их пересечения (если они существуют) являются точками пересечения прямой и конуса. Найдем горизонтальные проекции этих точек - М₂ и N₂, и, по соответствию их фронтальные проекции - М₂ и N₂ (рис. 8.12).

Трехмерная модель отыскания точек пересечения приведена на рисунке 8.13.

 

Рисунок 8.11 – Построение отрезков A1S1 и B1S1	Рисунок 8.12 – Отыскание точек пересечения прямой и конуса

 

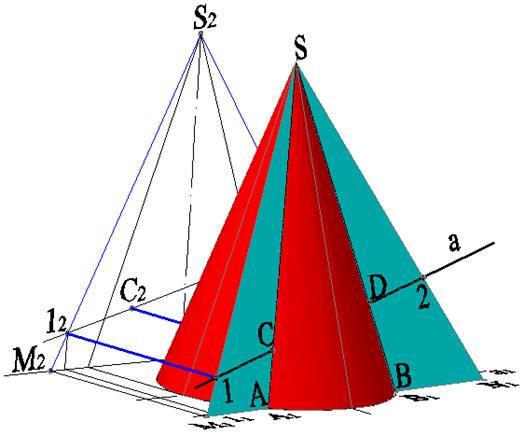
Рисунок 8.13 – Трехмерная модель отыскания точек пересечения

Приложение А

Варианты заданий к лабораторной работе № 1

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ Б

 

Варианты заданий к лабораторным работам № 2-4

 

№	А	В	С	Д
	40,5,55	0,50,10	65,20,0	70,65,60
	20,10,20	75,20,50	90,85,0	30,50,45
	85,20,80	25,40,20	90,90,30	70,10,10
	85,42,0	25,62,20	0,10,40	35,35,58
	10,20,25	55,50,10	80,0,65	40,50,45
	65,25,70	0,40,40	90,90,15	15,70,100
	40,70,5	0,30,30	65,25,65	20,80,65
	42,72,0	0,32,33	75,40,55	15,65,60
	55,0,30	0,10,60	5,55,15	35,35,50
	45,55,10	0,25,35	60,10,60	80,30,35
	45,0,60	80,45,15	15,10,10	10,60,55
	0,65,0	15,20,50	70,10,20	60,50,45
	25,30,50	65,50,10	10,60,40	0,30,15
	88,50,10	62,0,60	20,0,30	28,34,50
	0,50,10	25,0,60	70,5,30	60,35,70
	105,0,95	80,75,30	0,30,15	15,70,100
	40,65,20	0,10,60	55,20,40	65,15,30
	70,20,10	25,50,30	0,10,50	60,40,45
	0,15,40	60,60,75	85,45,10	50,5,45
	35,70,0	60,40,20	20,25,45	70,85,50
	25,5,70	65,30,30	0,45,25	45,65,80
	25,15,60	65,50,15	0,80,10	50,75,50
	70,25,5	15,55,35	20,5,50	50,75,40
	15,70,0	60,40,20	0,25,45	0,45,10
	30,55,5	75,10,50	5,0,20	0,35,65
	0,10,55	15,60,10	70,30,15	60,55,40
	25,30,30	65,10,50	10,20,90	0,55,45
	85,0,65	60,65,10	0,30,20	50,35,10
	70,5,65	10,20,30	50,50,20	20,65,10
	50,5,70	10,30,30	75,40,20	20,65,75

 

ПРИЛОЖЕНИЕ В

Варианты заданий к лабораторным работам № 5-7

 

№	Призма и пирамида	Конус и цилиндр	Центр основания	Высота	Плоскость сечения
Основание (фигура)	Длина сторон(ы)	Радиус основания	Угол наклона плоскости к оси х,°	Координата пересечения плоскости с осью х
	Правильный шестиугольник			(0,45,10)
	ромб			(20,50,10)
	Равносторонний треугольник			(15,40,20)
	Правильный пятиугольник			(10,45,20)
	Прямоугольник	40,15		(0,40,25)
	Параллелограмм	20,30, угол=40°		(0,55,20)
	Равносторонний треугольник			(15,30,30)
	Квадрат			(15,30,15)
	Правильный пятиугольник			(15,80,30)
	Прямоугольник	24,25		(5,50,40)
	Ромб			(10,45,10)
	Равносторонний треугольник			(15,50,10)
	Правильный пятиугольник			(45,70,30)
	Прямоугольник	25,35		(10,30,10)
	Параллелограмм	20,45, угол=35°		(15,60,30)
	Прямоугольный треугольник	катеты=25,18		(35,30,10)
	Квадрат			(25,20,20)
	Ромб			(30,30,30)
	Правильный шестиугольник			(10,25,40)

 

	Равносторонний треугольник			(5,40,10)
	Правильный пятиугольник			(20,50,20)
	Прямоугольник	24,15		(15,10,20)
	Параллелограмм	23,34, угол=20°		(10,15,30)
	Прямоугольный треугольник	катеты=20,30		(30,30,10)
	Квадрат			(30,35,10)
	Прямоугольник	21,26		(5,40,20)
	Ромб			(35,30,20)
	Равносторонний треугольник			(5,30,25)

 

 

ПРИЛОЖЕНИЕ Д

Варианты заданий к лабораторной работе № 8

№	Пирамида	Конус	Центр основания	Высота	Пересекащая прямая
Основание (Фигура)	Длина сторон(ы)	Радиус основания	Начальная коорд.	Конечная коорд.
	Правильный шестиугольник			(0,45,10)		(30,30,18)	(-40,60,60)
	Ромб			(20,50,10)		(40,5,5)	(0,65,55)
	Равносторонний треугольник			(25,40,20)		(50,45,15)	(0,20,60)
	Правильный пятиугольник			(30,45,20)		(40,10,15)	(10,50,60)
	Прямоугольник	40,15		(0,40,25)		(20,10,15)	(0,50,60)
	Параллелограмм	20,30, угол=40°		(0,55,20)		(10,20,50)	(-10,60,20)
	Равносторонний треугольник			(15,30,30)		(30,35,25)	(10,5,60)
	Квадрат			(15,30,15)		(30,20,18)	(-40,50,60)
	Правильный пятиугольник			(15,80,30)		(40,85,5)	(0,5,55)
	Прямоугольник	24,25		(5,50,40)		(50,45,15)	(0,20,60)
	Ромб			(10,45,10)		(40,10,15)	(10,50,60)
	Равносторонний треугольник			(15,50,10)		(20,10,15)	(0,50,60)
	Правильный пятиугольник			(45,70,30)		(10,20,50)	(-10,60,20)
	Прямоугольник	25,35		(10,30,10)		(30,35,25)	(10,5,50)
	Параллелограмм	20,45, угол=35°		(15,60,30)		(30,30,18)	(-40,60,60)
	Прямоугольный треугольник	катеты=25,18		(25,30,80)		(40,5,5)	(0,65,55)
	Квадрат			(25,20,20)		(50,45,15)	(0,10,45)
	Ромб			(30,30,30)		(40,10,15)	(10,50,60)
	Правильный шестиугольник			(10,15,40)		(20,10,15)	(0,50,60)
	Равносторонний треугольник			(5,40,10)		(10,20,50)	(-10,60,20)

 

	Правильный пятиугольник			(20,50,20)		(30,35,25)	(10,5,60)
	Прямоугольник	24,15		(15,10,20)		(40,10,15)	(0,50,65)
	Параллелограмм	23,34, угол=20°		(10,15,30)		(30,30,18)	(-40,60,60)
	Прямоугольный треугольник	катеты=20,30		(30,30,10)		(40,5,5)	(0,65,55)
	Квадрат			(30,35,10)		(50,45,15)	(0,20,60)
	Прямоугольник	21,26		(5,40,20)		(40,10,15)	(10,50,60)
	Ромб			(35,30,20)		(20,10,15)	(0,50,60)
	Равносторонний треугольник			(5,30,25)		(10,20,50)	(-10,60,20)
	Квадрат			(0,40,30)		(30,35,25)	(10,5,60)
	Правильный пятиугольник			(35,50,10)		(45,20,5)	(10,70,70)