Построение сечения прямой призмы фронтально-проецирующей плоскостью с помощью AutoCAD

Цель: приобретение навыков нахождения натуральной величины сечения прямой призмы методом замены плоскостей.

Контрольные вопросы:

 

1. Какой вид имеет сечение многогранника.

2. В каком случае проекция сечения прямой призмы определяется по чертежу без дополнительных построений?

Задание 1:методом замены плоскостей проекций найти натуральную величину сечения прямой призмы фронтально-проецирующей плоскостью; объекты заданы проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении В).

 

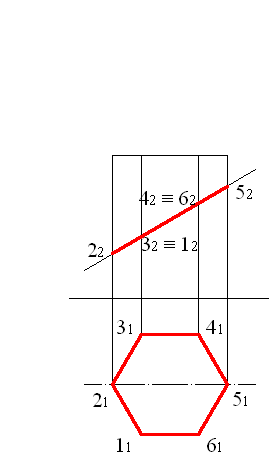
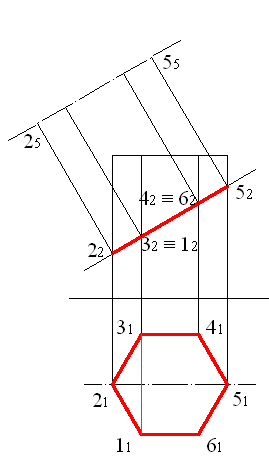
Решим задачу с помощью однократной замены плоскостей проекций. Фигура сечения представляет собой шестиугольник, который изображается на фронтальной плоскости проекций отрезком прямой, а на горизонтальной плоскости проекций как многоугольник, совпадающий с горизонтальной проекцией призмы (рис. 5.1).

Спроецируем ось симметрии на дополнительную плоскость, для этого

с помощью команды OFFSET, проводим штрих-пунктирную линию, параллельную фронтальному следу секущей плоскости (рис. 5.2). Расстояние между параллельными линиями может быть любым, рекомендуется выбрать его так, чтобы результат построения не накладывался на фронтальную проекцию призмы.

Рисунок 5.1 – Проекции сечения прямой шестигранной призмы	Рисунок 5.2 – Проецирование оси симметрии на дополнительную плоскость

 

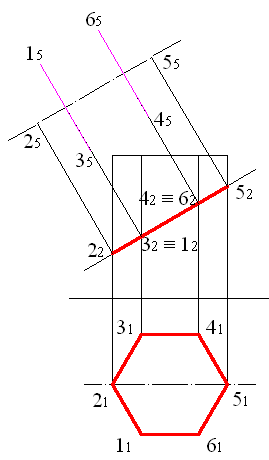
Теперь можно найти проекции точек 1 – 6 на дополнительную плоскость:

- построим перпендикуляры из точек 2₂, 3₂, 4₂ и 5₂ (рис. 5.3) на ось симметрии, при этом будут получены проекции точек 2 и 5;

- чтобы построить проекции точек 1, 3, 4 и 6, найдем расстояние между точками 1 и 3, для этого соединим горизонтальные проекции этих точек отрезком (рис. 5.4), длина отрезка будет равна расстоянию между точками, т.к. он параллелен горизонтальной плоскости;

Рисунок 5.3 – Проецирование точек 2 и 5	Рисунок 5.4 – Отыскание расстояния между точками 1 и 3

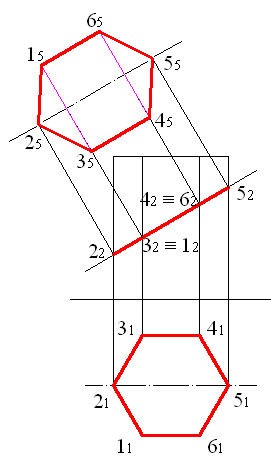
- с помощью команды ALIGN построим проекцию полученного отрезка на плоскость П₅, таким образом, будут найдены точки 1₅ и 3₅ (рис. 5.5);

- учитывая, что расстояние между точками 4 и 6 в данном случае совпадает с расстоянием между точками 1 и 3, скопируем полученный отрезок и получим точки 4₅ и 6₅ (рис. 5.6).

Рисунок 5.5 – Построение проекций точек 1 и 3	Рисунок 5.6 – Построение проекций точек 4 и 6

 

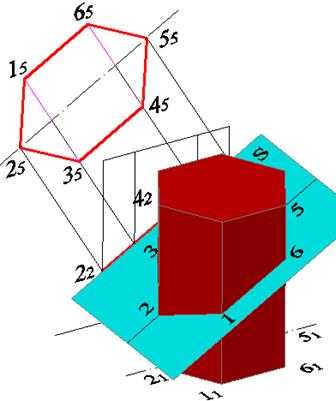
Так как плоскость П₅ параллельна секущей плоскости, точки 1₅, 2₅, 3₅, 4₅, 5₅ и 6₅ являются вершинами шестиугольника, представляющего собой натуральную величину сечения (рис. 5.7).

На рисунке 5.8 приведена трехмерная модель рассмотренного построения.

На рисунке 5.9 показан случай, когда секущая плоскость проходит через верхнее основание призмы.

В случае, если основание призмы не имеет оси симметрии, следует провести линию из крайней слева или справа вершины, затем измерять и откладывать на плоскость П₅ расстояния до нее (рис 5.10).

 

Рисунок 5.7 – Построение сечения	Рисунок 5.8 – Трехмерная модель

 

Рисунок 5.9 – Построение сечения в случае, когда пересекается основание	Рисунок 5.10 – Отсутствие оси симметрии

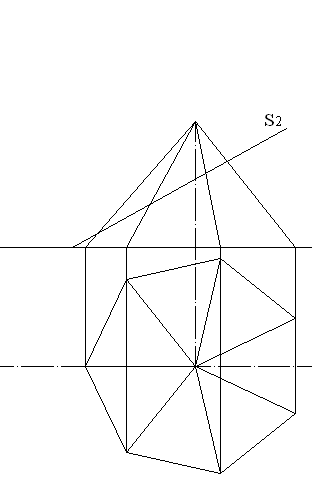
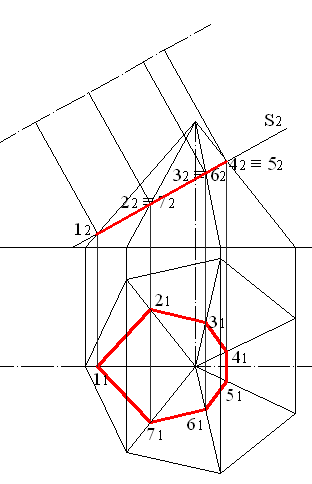
Задание 2:методом замены плоскостей проекций найти натуральную величину сечения пирамиды фронтально-проецирующей плоскостью; (варианты заданий приведены в приложении В).

Рассмотрим отыскание натуральной величины сечения семиугольной пирамиды фронтально-проецирующей плоскостью. Исходный чертеж приведен на рис. 5.11. В отличие от рассмотренного выше случая, горизонтальная проекция сечения не совпадает с проекцией основания. Ее необходимо найти, используя фронтальные проекции точек пересечения ребер с секущей плоскостью, горизонтальные проекции этих точек определяем по соответствию (рис. 5.12). Сечение представляет собой семиугольник, вершины его – точки 1, 2, 3, 4, 5, 6, 7.

Рисунок 5.11 – Пирамида и секущая плоскость	Рисунок 5.12 – Горизонтальная проекция сечения пирамиды

 

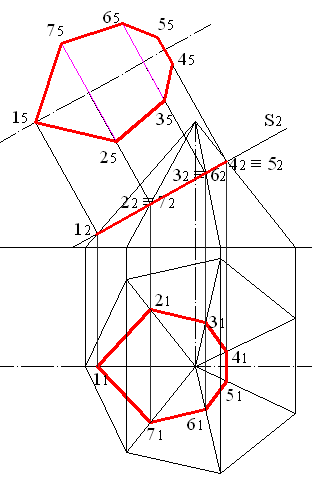
Для отыскания натуральной величины сечения построим проекцию осевой линии на плоскость, параллельную сечению. Опустим на нее перпендикуляры из фронтальных проекций точек пересечения ребер с секущей плоскостью (рис. 5.13). Построим отрезки, определяющие расстояние между точками 2 и 7, 3 и 6, 4 и 5. Эти отрезки параллельны горизонтальной плоскости, поэтому построим их между горизонтальными проекциями вышеупомянутых точек. Спроецируем полученные отрезки на плоскость П₅, семиугольник, определяемый точками 1₅, 2₅, 3₅, 4₅, 5₅, 6₅ и 7₅ представляет собой натуральную величину сечения (рис. 5.14).

Рисунок 5.13 – Проецирование осевой линии	Рисунок 5.14 – Натуральная величина сечения

 

Лабораторная работа №6