Отыскание точки пересечения прямой и плоскости средствами AutoCAD.

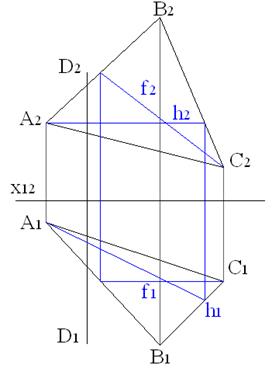
Цель: приобретение практических навыков отыскания перпендикуляра из точки на плоскость, заданную треугольным отсеком, с использованием главных линий плоскости и свойств прямого угла;

получение навыков нахождения точки пересечения прямой и плоскости, заданной треугольным отсеком, с помощью средств AutoCAD.

Контрольные вопросы:

1. Что такое фронталь и горизонталь?

2. Каковы признаки перпендикулярности прямой и плоскости?

3. Какие линии плоскости целесообразно использовать для построения перпендикуляра к плоскости?

4. Назовите виды взаимного положения прямой и плоскости.

5. Как использовать вспомогательную секущую плоскость для решения поставленной задачи?

6. Почему целесообразно использовать проецирующую секущую плоскость?

Задание 1:найти направление перпендикуляра от точки D до плоскости треугольного отсека ABC; точка и треугольный отсек заданы проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении Б).

Построим проекции точки D и треугольного отсека ABC, задающего плоскость (рис. 3.1).

Строим горизонтальную и фронтальную проекции горизонтали h и фронтали f плоскости (см. рис. 3.2):

- используя команду LINE, привязку ENDPOINT и режим построения ORTHO, строим фронтальную проекцию горизонтали h₂ из точки A₂ и горизонтальную проекцию фронтали f₁ из точки C₁;

- используя привязку INTERSEC и режим построения ORTHO из точки пересечения h₂ с B₂C₂ инструментом LINE проводим вертикальную линию связи до пересечения с B₁C₁;

- используя команду LINE, привязку ENDPOINT строим горизонтальную проекцию горизонтали h₁ из точки A₁;

- используя привязку INTERSEC и режим построения ORTHO из точки пересечения f₁ с A₁B₁ инструментом LINE проводим вертикальную линию связи до пересечения с A₂B₂;

- инструментом LINE строим фронтальную проекцию фронтали f₂ из точки C₂;

Из точки D проводим проекции перпендикуляра. Используя привязку PERPEND, строим с помощью инструмента LINE:

- горизонтальную проекцию перпендикуляра перпендикулярно к горизонтальной проекции горизонтали на П₁;

- фронтальную проекцию перпендикуляра перпендикулярно к фронтальной проекции фронтали на П₂ (для построения перпендикуляра к фронтальной проекции фронтали ее необходимо продлить с помощью команды Lengthen).

Результат построения изображен на рисунке 3.3.

Рисунок 3.1 – Изображение плоскости, заданной треугольным отсеком ABC и точки D	Рисунок 3.2 – Результат построения горизонтальной и фронтальной проекций горизонтали h и фронтали f плоскости

Рисунок 3.3 – Направление перпендикуляра из точки D на плоскость ABC

Задание 2:найти точку пересечения перпендикуляра и плоскости, заданной треугольным отсеком ABC с помощью средств AutoCAD.

 

Задача, отыскания точки пересечения прямой и плоскости решается способом сечения (прямая заключается в вспомогательную секущую плоскость) – это основная позиционная задача инженерной графики.

 

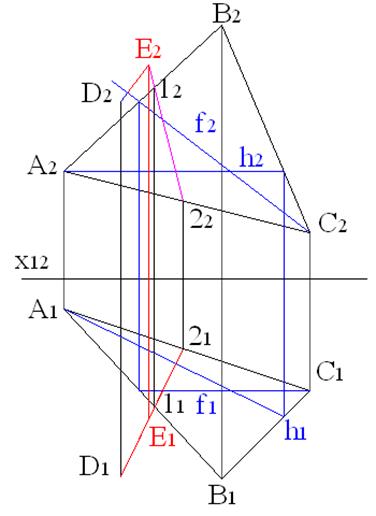
Определяем основание перпендикуляра с помощью секущей горизонтально проецирующей плоскости, которая пересечет отсек по прямой 1-2:

- c помощью команды EXTEND продляем горизонтальную проекцию перпендикуляра до пересечения с A₁C₁ и отмечаем точки 1₁ и 2₁, в которых прямая 1-2 пересечет горизонтальные проекции сторон АB и AС;

- по вертикальному соответствию строим точки 1₂ и 2₂ на соответствующих фронтальных проекциях сторон АB и AС треугольного отсека;

- используя команду LINE и привязку ENDPOINT, соединяем точки 1₂ и 2₂;

- отыскиваем E₂ – точку пересечения фронтальной проекции перпендикуляра и линии 1₂-2₂ (в данном примере для ее отыскания нужно продлить фронтальную проекцию перпендикуляра до пересечения с продолжением 1₂-2₂);

- по вертикальному соответствию находим точку E₁.

Получим: основание перпендикуляра - точку Е и проекции отрезка, длина которого равна расстоянию от точки до плоскости – D₁E₁ и D₂E₂ (см. рис. 3.4). Точка Е – точка пересечения прямой с плоскостью.

Заметим, что в рассмотренном примере точка Е оказалась за пределами проекций треугольного отсека, задающего плоскость. Такую ситуацию не следует считать ошибочной.

Рисунок 3.4 – Е – точка пересечения прямой и плоскости

Лабораторная работа №4

 

Преобразования чертежа.

Цель: приобретение практических навыков применения способов преобразований чертежа для решения метрических задач.

 

Контрольные вопросы:

 

1. Каким должно быть положение плоскости для того чтобы воспользоваться методом замены плоскостей?

2. В чем состоит суть метода замены плоскостей проекций?

 

Задание 1:найти расстояние от точки D до плоскости треугольного отсека ABC; точка и треугольный отсек заданы проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении Б).

Найдём расстояние от точки до плоскости методом замены плоскостей проекций.

Эта задача решается с помощью однократной замены плоскости проекций, после которой треугольник будет проецирующим.

На рисунке 4.1 изображены проекции точки D и плоскости, заданной треугольным отсеком ABC.

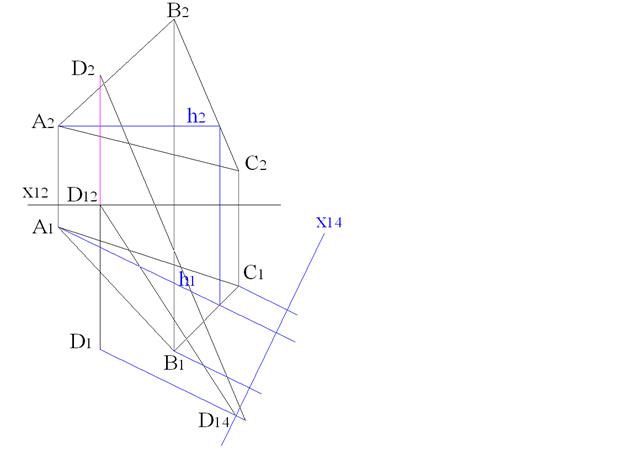
Рисунок 4.1 – Изображение проекций плоскости, заданной треугольным отсеком ABC и точки D

Строим горизонталь плоскости ABC h (рис. 4.2):

- в режиме ORTHO строим h₂ из точки A₂ до пересечения со стороной B₂C₂;

- в режиме ORTHO и c применением привязки INTERSECTION опускаем линию связи до пересечения с B₁C₁;

- c применением привязки INTERSECTION строим h₁ от точки A₁ до полученной точки пересечения;

- с помощью команды LENGTHEN продляем горизонтальную проекцию горизонтали так, чтобы удобно было строить след дополнительной плоскости.

Рисунок 4.2 – Результат построения горизонтальной проекции горизонтали h

След дополнительной плоскости x₁₄ проводим перпендикулярно к горизонтальной проекции горизонтали, что в силу свойств проекций прямого угла обеспечивает перпендикулярность этой плоскости горизонтали, а, следовательно, и плоскости ABC. Для этого:

- с помощью команды LINE с применением привязки PERPEND проводим линию x₁₄ перпендикулярно проекции h₁;

- продляем x₁₄ с помощью команды LENGTHEN так, чтобы перпендикуляры из точек D₁, B₁ и C₁ к этой линии заканчивались на ней, а не на её продолжении;

- с помощью команды LINE проводим вышеупомянутые перпендикуляры с применением привязки PERPEND;

- с помощью команды LENGTHEN продляем концы перпендикуляров (рис. 4.3).

Рисунок 4.3 – Замена плоскости (новая ось x₁₄)

Новая плоскость П₄ перпендикулярна плоскости треугольника, следовательно его проекция на эту плоскость – прямая линия A₄B₄C₄ . Построим эту проекцию и проекцию точки D – D₄ . Для этого перпендикулярно оси x₁₄ отложим отрезки, равные расстояниям от проекций вершин треугольника A₂, В₂ и С₂ и точки D₂ до оси x₁₂.

Опишем это построение для точки D. Построим отрезок D₂D₁₂. При помощи команды ALIGN совместим точку D₁₂ с точкой D₁₄, а точку D₂ с концом продленного отрезка D₁D₁₄ (рис.4.4). Применим команду ALIGN, в ответ на вопрос “select objects:” выберем построенный отрезок, далее:

Specify first sourse point - точка D₁₂;

Specify first destination point - точка D₁₄;

Specify second sourse point - точка D₂;

Specify second destination point – конец продленного отрезка;

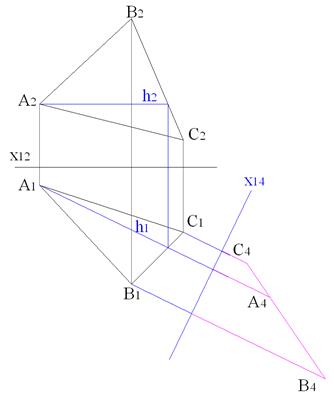
Рисунок 4.4 – Совмещение точек

Specify third sourse point or <continue> - ENTER;

Scale objects based on alignment points [Yes/No] – ENTER.

Результат приведен на рисунке 4.5.

Таким же способом получим проекции точек A, B и C на плоскость П₄. Точки C₄ и B₄ соединим прямой и получим новую проекцию треугольника ABC - A₄B₄C₄. Проведем перпендикуляр из точки D₄ к прямой A₄B₄C₄, длина его будет равна расстоянию от точки D до плоскости ABC (рис. 4.6).

Рисунок 4.5 – Проекция точки D на плоскость П₄

Рисунок 4.6 – Результат нахождения расстояния от точки до плоскости

 

Задание 2:методом замены плоскостей проекций найти натуральную величину треугольника ABC, заданного проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении Б).

 

Решим задачу с помощью двух последовательных замен плоскостей: после первой замены треугольник будет проецирующим, а после второй - параллельным дополнительной плоскости.

Треугольник задан проекциями на горизонтальную и фронтальную плоскости (рис. 4.7). Проецирование на плоскость П₄, перпендикулярную треугольнику, выполняется так же, как для задания 1.

Рисунок 4.7 – Проекции треугольника	Рисунок 4.8 – Построение горизонтали

 

 

Рисунок 4.9 – Замена плоскости (новая ось x14)	Рисунок 4.10 – Проецирование треугольника на плоскость П4

 

Заменяем плоскость проекций П₁ плоскостью П₅, которая параллельна плоскости треугольника:

- при помощи команды LINE проведем линию через точки А₄, В₄ и С₄ и переместим ее с помощью параллельного переноса (команда MOVE), получим ось x₄₅, параллельную проекции A₄B₄C₄ (можно использовать также команду OFFSET), ось x₄₅ на рисунке 4.11 продлена в обе стороны для наглядности;

- используя привязку PERPEND, построим с помощью команды LINE перпендикуляры из точек А₄, В₄ и С₄ к оси x₄₅ и продлим их с помощью команды LENGTHEN (рис. 4.11).

Рисунок 4.11 – Второй этап замены плоскостей

 

Выполненная замена обеспечивает проецирование треугольника на новую плоскость в натуральную величину:

- от оси x₄₅ на соответствующих вспомогательных прямых откладываем отрезки, равные расстояниям от проекций вершин треугольника A₁, В₁ и С₁ до оси x₁₄ при помощи команды ALIGN;

- полученные точки соединим отрезками с помощью команды LINE и получим новую проекцию треугольника ABC - A₅B₅C₅, которая представляет треугольник АВС в натуральную величину (рис. 4.12).

Рисунок 4.12 – Результат нахождения натуральной величины треугольника

 

Задание 3: методом вращения вокруг линии уровня найти натуральную величину треугольника ABC, заданного проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении Б).

Решим задачу с помощью вращения треугольника ABC (рис. 4.13) вокруг его горизонтали h (рис. 4.14).

Рисунок 4.13 –Треугольник ABC	Рисунок 4.14 – Горизонталь треугольника

 

Определяем радиус окружности по дуге которой вращается точка B:

- из точки В₁ проводим прямую, перпендикулярную к h₁ (рис. 4.15), здесь учитывается, что горизонтальная проекция точки движется перпендикулярно проекции оси вращения;

- построив отрезок с помощью команды LINЕ, замеряем расстояние от В₂ до h₂;

- с помощью команды ALIGN откладываем полученный отрезок от точки В₁ в направлении, перпендикулярном прямой, построенной на предыдущем шаге;

- с помощью команды ROTATE поворачиваем этот отрезок на 90 градусов;

- искомый радиус вращения получим, соединив конечную точку построенного отрезка с точкой пересечения прямой, проведенной перпендикулярно горизонтальной проекции горизонтали h₁ и горизонтальной проекцией горизонтали(см. рис. 4.15).

Найдем положение точки В₁' (после поворота точка B и горизонталь задают плоскость, параллельную П₁):

- построим окружность найденного радиуса и продлим отрезок B₁1₁ до пересечения с ней (см. рис. 4.16);

- для наглядности удалим лишнюю часть окружности с помощью команды TRIM.

Рисунок 4.15 – Радиус дуги вращения точки В	Рисунок 4.16 –Точка В после поворота

 

Заметим, что точка A находится на оси вращения, таким образом, остаётся найти положение точки C после поворота – C₁'. Для этого её можно было бы повернуть как точку B, но возможен другой путь. Примем во внимание, что точка 1 находится на пересечении оси вращения (горизонтали h)
и стороны BC. Поэтому можно построить отрезок В₁'1₁,который будет представлять часть стороны BC после поворота. Точка C лежит на этой прямой, но она должна находиться и на перпендикуляре к оси вращения. Следовательно, точка C₁' находится на пересечении продолжения отрезка В₁'1₁ и этого перпендикуляра (рис 4.17).

Рисунок 4.17 – Положение точки C после вращения

 

Для построения натуральной величины треугольника с помощью команды LINE с применением привязки ENDPOINT соединим точки А₁, В₁' и С₁' (рис. 4.18). Треугольник А₁В₁'С₁' - натуральная величина треугольника АВС.

Рисунок 4.18 – Натуральная величина треугольника ABC

 

Задание 4:методом замены плоскостей проекций найти расстояние между скрещивающимися прямыми AB и CD, заданных проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении Б).

 

Решим задачу с помощью последовательной замены плоскостей проекций, в результате чего одна из прямых будет преобразована в проецирующую.

На рисунке 4.19 прямые AB и CD, заданы проекциями на горизонтальную и фронтальную плоскость.

Рисунок 4.19 – Проекции скрещивающихся прямых

Последовательной заменой плоскостей проекций преобразуем прямую CD в проецирующую. Одновременно в системе новых плоскостей проекций будут построены проекции второй прямой АВ.

Выполним первую замену плоскостей проекций:

- включить режим привязки с помощью F3, либо нажать вкладку OSNAP;

- инструментом LINE проводим ось x₁₄ параллельную проекции прямой С₁D₁ , используя объектную привязку ;

- проводим вспомогательные прямые из точек A₁, B₁, C₁, D₁ перпендикулярно оси x₁₄, используя объектную привязку (см. рис. 4.20);

- удлиняем отрезки при помощи команды LENGTHEN;

 

Рисунок 4.20 – Построение следа плоскости, параллельной прямой CD

- от оси x₁₄ на соответствующих вспомогательных прямых откладываем отрезки, равные расстояниям от проекций точек A₂, В₂, С₂ и D₂ до оси x₁₂ при помощи команды выравнивания ALIGN. Для указания точек источника и точек целевого объекта используем объектную привязку к конечной точке отрезка ;

- полученные точки соединим линиями и получим новые проекции прямых AB и CD - A₄B₄ и С₄D₄ (см. рис. 4.21).

Рисунок 4.21 – Проецирование прямых АВ, СD на плоскость проекций П₄

Выполняем вторую замену плоскостей проекций:

- используя команду LINE, проведем линию перпендикулярную продолжению С₄D₄, получим ось x₄₅;

- используя привязку, построим вспомогательные прямые из точек А₄, В₄, С₄ и D₄ перпендикулярно оси x₄₅ (рис. 4.22) (для проведения перпендикулярных линий необходимо использовать объектную привязку );

Рисунок 4.21 – Второй этап замены плоскостей проекций

 

После такой замены плоскостей проекций прямая CD спроецируется в точку, а перпендикуляр, опущенный из этой точки на проекцию прямой АВ на плоскость П₅, будет искомым расстоянием:

- от оси x₄₅ на соответствующих вспомогательных прямых откладываем отрезки, равные расстояниям от проекций точек A₁, В₁, С₁и D₁ до оси x₁₄ при помощи команды выравнивания ALIGN, используя объектную привязку к конечной точке отрезка ;

- полученные точки соединим линиями командой LINE и получим проекции прямых AВ и CD – A₅В₅ и C₅D₅ (прямая CD проецируется в точку C₅=D₅);

- опустив перпендикуляр из точки C₅=D₅ на отрезок A₅В₅, получим искомое расстояние между скрещивающимися прямыми (рис. 4.23).

Рисунок 4.23 – Расстояние между скрещивающимися прямыми АВ и CD

Лабораторная работа №5