Построение сечения конуса плоскостью

Цель:найти натуральную величину сечения прямого кругового конуса методом замены плоскостей.

 

Контрольные вопросы:

1. Перечислите виды сечения кругового конуса?

Задание:методом замены плоскостей проекций найти натуральную величину сечения прямого кругового конуса фронтально-проецирующей плоскостью; объекты заданы проекциями на горизонтальную и фронтальную плоскость (варианты заданий приведены в приложении В).

 

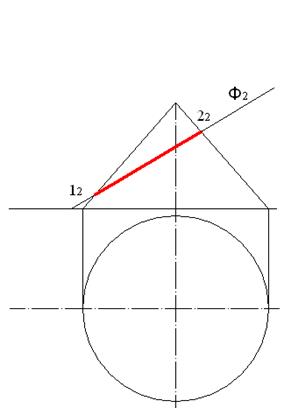
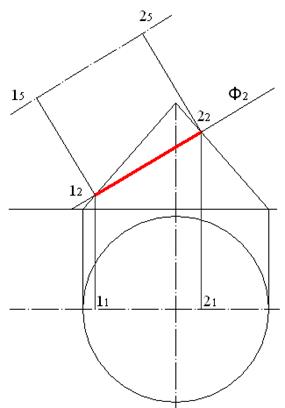
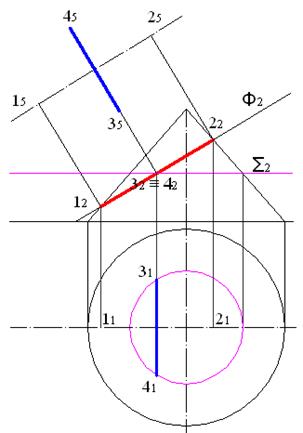
Решим задачу с помощью однократной замены плоскостей проекций. Фигура сечения представляет собой эллипс, который изображается на фронтальной плоскости проекций отрезком прямой, а на горизонтальной плоскости проекций - эллипсом.

Исходные данные для решения задачи приведены на рисунке 7.1.

Заметим, что фронтальная проекция сечения задается отрезком 1₂ – 2₂ и ее длина определяет длину одной из осей искомого эллипса. Построим проекцию осевой линии на плоскость П₅ и найдем проекцию оси 1-2 на эту плоскость и на горизонтальную плоскость (рис. 7.2).

Рисунок 7.1 – Проекции конуса и фронтально проецирующей плоскости Ф	Рисунок 7.2 – Проекции оси эллипса на плоскость П5 и на горизонтальную плоскость

 

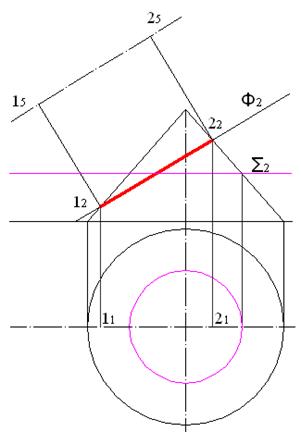
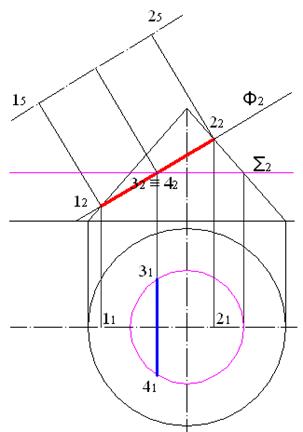
Вторая ось эллипса представляет собой фронтально-проецирующий горизонтальный отрезок, его фронтальная проекция представляет собой точку в середине отрезка 1₂ – 2₂. Для определения длины этой оси проведем через эту точку вспомогательную фронтально-проецирующую горизонтальную плоскость Σ. Плоскость Σ пересекает конус по окружности, на рисунке 7.3 показано, как определить ее радиус и построить горизонтальную проекцию. Вторая ось эллипса лежит в плоскости этой окружности и касается поверхности конуса в точках 3 и 4. На рисунке 7.4 показано отыскание горизонтальных проекций этих точек. Отрезок 3₂ – 4₂ определяет длину второй оси эллипса.

 

Рисунок 7.3 – Построение плоскости Σ	Рисунок 7.4 – Определение длины второй оси эллипса

 

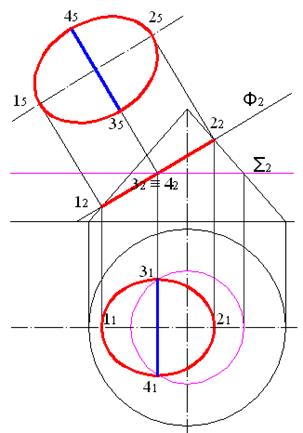
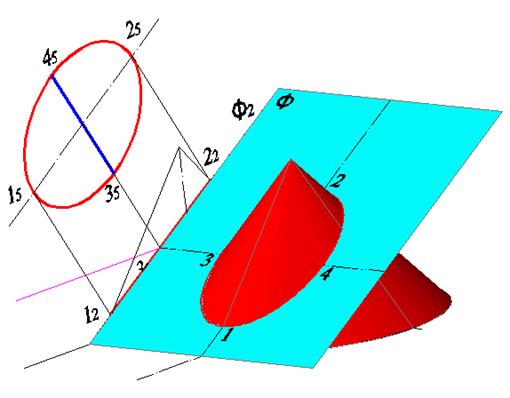
Построим проекцию оси 3-4 на плоскость П₅, для этого, как и в предыдущих лабораторных работах, применим команду ALIGN. Результат приведен на рисунке 7.5. Для наглядности горизонтальная проекция оси восстановлена.

На рисунке 7.6 показан результат построения натуральной величины сечения в виде эллипса, заданного осями 1₅ – 2₅ и 3₅ – 4₅. На этом же рисунке построена горизонтальная проекция сечения, это тоже эллипс, заданный осями 1₁ – 2₁ и 3₁ – 4₁.

Трехмерная модель сечения приведена на рисунке 7.7.

Рисунок 7.5 – Проекция второй оси эллипса на плоскость П5	Рисунок 7.6 – Натуральная величина сечения конуса

Рисунок 7.7 – Трехмерная модель сечения

Если секущая плоскость пересекает основание конуса, следует продлить коническую поверхность так, чтобы плоскость пересекала все образующие. Это даст возможность построить сечение в виде эллипса и высечь из него эллиптическую дугу, представляющую сечение заданного конуса (рис. 7.8). Это можно сделать с помощью команды TRIM, воспользовавшись в качестве секущих кромок отрезками 5₅ – 6₅ (для натуральной величины сечения) и 5₁– 6₁ (для горизонтальной проекции сечения).

Рисунок 7.8 – Сечение в виде эллиптической дуги

Трехмерная модель для этого случая приведена на рисунке 7.9.

Рисунок 7.9 – Трехмерная модель сечения в виде эллиптической дуги

 

 

Лабораторная работа №8