Матрицы для Е и i
Матрицы, описывающие операции идентичности и инверсии для точки общего положения P (X, Y, Z) очень логичны. В результате операции идентичности все координаты останутся на своих местах,и операции инверсии относительно центра, расположенного в начале координат (0,0,0) переведут точку (X, Y, Z) в положение (- X, -Y, -Z).
Матрицы для операцийЕ и I приведены ниже.
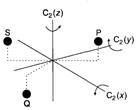
Последовательные операции симметрии в точечной группе D2 Теперь у нас есть возможность анализировать эффект от проведения последовательных операций симметрии и с помощью изображений и с помощью использования простых матриц. Одна из наиболее лёгких для понимания систем возникает, когда все важные операции симметрии включают простое вращение. На Рис. 2.5 показана точка общего положения P (X, Y, Z) в системе Декартовых координат,
где оси С2 лежат вдоль направлений x, y, z каждая. Совокупность этих эелементов вместе с идентичностью составляет точечную группуD2. Вращение относительно x посредством С2 (x) переведёт Р в положение Q с координатами (X, -Y, -Z), и последующее вращение относительно у с помощью С2 (у) спроецирует Q в точку S c координатами (- X, -Y, Z). Если затем мы проведём операцию поворота относительно С2 (z) к точке S. Мы вернёмся в из начальную позицию Р. Отдельные операции могут быть записаны как: C2 (x)P ® Q, C2 (y) Q ® S, C2 (z)S ® P А полная последовательность операций как: C2 (z) * C2 (y) *C2 (x)P ® P Отметим, что первая из проведенных операций, С2 (x) при записи последовательных операций находится правее всех. Эти последовательные операции иллюстрируют одну из наиболее важных особенностей точечных групп: результат проведения двух или более последовательных операций может в большинстве случаев получиться независимым применениям другой операции из группы. В данном случае, результат двух первых операций C2 (y) *C2 (x)P ® S может быть получен при помощи C2 (z)P ® S, т.е. C2 (y) *C2 (x) = C2 (z) Полная последовательность C2 (z) * C2 (y) *C2 (x) эквивалентна Е.
|