Приводимые представления

 

Наборы чисел, которые определяли эти четыре представления, это единственные такие числа, которые подчиняются данной таблице умножения, за исключением набора нулей,

Рис. 3.1

однако не так уж и трудно найти наборы матриц, которые будут вести себя аналогично. Если мы рассмотрим приведенную на Рис. 3.1. матрицу 2 х 2, то следуя описанным ранее правилам умножения матриц, мы можем увидеть, что:

И, в результате, такая матрица может занимать место каждой из операций симметрии Е, C₂ (z), σ_v (xz) и σ _v' (yz) в таблице умножения для группы C_2v.Четыре таких матрицы могут поэтому составлять представление тем же самым путём, что и «числа» 1, 1, 1 и 1.

Однако, представление, сформированное такими матрицами, теперь является приводимым, а не неприводимыми, и может быть разбито на два более простых представления.

На Рис. 3.2 показано, как четыре приведенные выше матрицы 2 х 2 образуют

Рис. 3.2

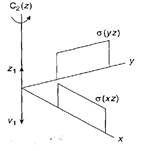
представление, если мы решили провести операции симметрии в точечной группе C_2v по отношению к векторам z₁ и n₁. Мы уже видели, что z₁ сам по себе может быть использован для иллюстрирования представления А₁, и то же самое очевидно для n₁ пока он не подвергается воздействию любой из операций симметрии. Если векторы z₁ и n₁. рассматривать вместе, результат может быть выражен, например, таким образом

Получающееся представление, которое может быть обозначено, как «Γ_zv», теперь выглядит так:

Очевидно, что это представление слагается из представления А₁ для z₁ и представления А₁ для n₁, и присутствие обеих этих компонентов показано ниже:

With the reduction step можно заключить, то Γ_zv=2А₁.

На рисунке 3.3. установлен порядок действий для идентификации приводимого

Рис. 3.3

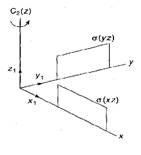
представления Г_xyz, которая описывает результат использования трёх векторов – x₁, y₁ и z₁ как базисов. Эти три матрицы составляю представление Г_xyz.

Возникшие теперь матрицы 3 х 3 идентичны тем, которые выводились ранее при рассмотрении эффекта, производимого различными операциями симметрии на точку P (X, Y, Z):

Здесь подобное объединение обнаруживает, что неприводимое представление имеет вид:

Г_xyz=В₁ + В₂ + А₁

_Это важное представление. Которое связано и с движением атомов и с симметрией атомных орбиталей.

На этих двух примерах становится ясно, что решение для каждого случая - уникально, и что для процесса приведение не существует других возможных решений. Это является главной особенностью приводимых представлений:

Приводимое представление даёт начало (служит источником) только одному набору неприводимых представлений.

 

3.2 Использование характеров матриц при приведении путём проверки (подстановки?)