Принципы распределения доходов населения
Распределение населения по среднедушевому денежному доходу имеет правостороннюю асимметрию и может быть одномодальным или бимодальным. В России бимодальное распределение появилось в области высоких денежных доходов, что свидетельствует о дифференциации среди высокодоходных групп населения. При образовании и стабилизации ''среднего класса'' бимодальность в распределении населения по доходу исчезает. В настоящее время в России ведётся поиск оптимальной модели для математического описания распределения населения по среднедушевому доходу в условиях переходной и рыночной экономики. Дифференциация доходов, как правило, рассматривается по размеру среднедушевого совокупного дохода населения в целом, отдельных регионов и групп домохозяйств (проживающих в городской местности, в сельской местности, из них хозяйств пенсионеров, имеющих детей до 16 лет). В статистике бюджетов домашних хозяйств используются среднемесячный совокупный доход и средний доход на одного члена домохозяйства. Среди работающих за основу берётся среднемесячная начисленная заработная плата рабочих и служащих по отраслям экономики (без работников, занятых неполные рабочий день или неделю, и учеников). Для изучения дифференциации доходов и потребления населения проводятся перегруппировки домохозяйств: - по децильным группам - выделяются десять групп, в каждой группе по 10% домохозяйств; - по квинтильным группам - пять групп, в каждой группе по 5% населения; - по покупательской способности населения - по группам, кратным величине прожиточного минимума или стоимости набора из 25 (или из 31) наименований продуктов питания. По каждой выделенной группе вычисляются: средний денежный доход, его состав; средний потребительский расход и его структура; средний размер потребления на душу населения продуктов питания, непродовольственных товаров и услуг (в расчёте на 100 домохозяйств); показатель покупательской способности денежных доходов (денежных доход, делённый на среднюю цену покупки данного товара). На основании распределения населения по размеру доходов рассчитываются следующие статистические характеристики: 1. Обобщающие показатели распределения: модальное значение дохода, медианное значение дохода и средний доход.
гдехМ0 –нижняя граница модального интервала; iМ0 – величина модального интервала; fМ0, fМ0-1, fМ0+1 – частоты (частости) соответственно модального, домодального и послемодального интервалов [1, с. 105].
Где хМе – начало медианного интервала; iМе – величина медианного интервала; ∑f - сумма частот (частостей) вариационного ряда; fМе – частота (частость) медианного интервала; SМе–1 – сумма накопленных частот (частостей) в домедианном интервале.
гдеn - вариант; х – число единиц в совокупности. 2. Показатели структуры распределения дохода: квартильный уровень дохода (нижний и верхний), децильный и другие возможные уровни дохода (нижние и верхние), доля квартильных, децильных и других групп населения (домохозяйств) по уровню дохода в денежном доходе общества, средний доход по выделенным группам населения. 3. Коэффициенты дифференциации доходов населения, устанавливающие размер повышения денежных доходов высокодоходных групп по сравнению с низкодоходными группами населения. К показателям дифференциации денежных доходов относятся: 1) децильный коэффициент дифференциации гдеd1 - значение аргумента (в данном случае дохода), вероятность быть ниже которого равна 0,1 (F1) (т.е. 10% населения имеют доход ниже этого значения); d9 - значение аргумента, вероятность быть ниже которого равна 0,9 (F9) (т.е. 10% населения имеют доход выше этого значения). 2) коэффициент фондов гдеS10 - суммарный доход, который приходится на 10% населения с самыми высокими доходами, S1 - суммарный доход, который приходится на 10% населения с самыми низкими доходами [1, с. 108]. 3) кривая Лоренца гдеyi - доля доходов, сосредоточенная у i-й социальной группы населения; xi - доля населения, принадлежащая к i-й социальной группе в общей численности населения; n- число социальных групп. 4) коэффициент Джини гдеcum yi - кумулятивная доля дохода. При их расчёте используются данные о доходах крайних (бедных и богатых) групп населения (децильный коэффициент, коэффициент фондов) или полностью распределение населения по доходам (кривая и коэффициент Лоренца и коэффициент Джини). Они относятся к системе оценок, известной как методология Парето - Лоренца - Джини, широко используемой в зарубежной социальной статистике. Итальянский статист и социолог В.Парето (1848-1923) обобщил данные некоторых стран и установил, что между уровнем доходов и числом их получателей существует обратная зависимость, названная законом Парето. Американский статистик и экономист О.Лоренц (1876-1959) развил этот закон, предложив его графическое изображение в виде кривой, получившей название ''кривая Лоренца''. Кривая Лоренца представляет собой кривую концентрации по группам. На графике Лоренца в случае равномерного распределения дохода попарные доли населения и доходов должны совпадать и располагаться на диагонали квадрата, что и означает полное отсутствие концентрации дохода. Отрезки прямых, соединяющие точки, соответствующие накопленным частостям и нарастающим процентам дохода, образуют ломаную линию концентрации (кривую Лоренца). Чем больше эта линия отличается от диагонали (чем больше её вогнутость), тем больше неравномерность распределения доходов, соответственно выше его концентрация. Очевидно, в конкретных случаях нельзя ожидать ни абсолютного равенства, ни абсолютного неравенства в распределении доходов среди населения. Коэффициент Лоренца как относительная характеристика неравенства в распределении доходов. Коэффициент концентрации доходов Джини показывает распределение всей суммы доходов населения между его отдельными группами. Коэффициент G изменяется в интервале от 0 до 1. Чем ближе значение G к 1, тем выше уровень неравенства (концентрации) в распределении совокупного дохода; чем ближе он к 0, тем выше уровень равенства.
|

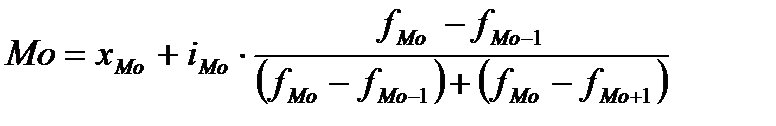 (1.1)
(1.1)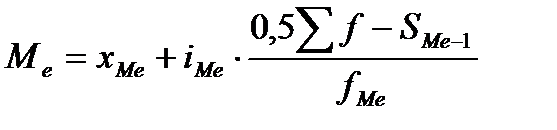 (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7)


