Степень выпускника: бакалавр
Киров Рассмотрено на заседании кафедры прикладной информатики и математики, протокол № 4 от 14 декабря 2012 г.
Утверждена на заседании учебно-методического совета, протокол № 73 от 21 января 2013 г. Математика: Методические указания / Сост. А.И. Глушкова. – Киров: ВСЭИ, 2013. – 32 с.
Методические указания разработаны в соответствии с учебной программой дисциплины «Математика» и предназначены для студентов, обучающихся по направлению подготовки 230700.62 Прикладная информатика (степень выпускника: бакалавр).
© Вятский социально-экономический институт (ВСЭИ), 2013
1. Цели и задачи контрольной работы Цель контрольной работы: изучение основных понятий высшей математики: линейной алгебры, аналитической геометрии, математического анализа. Задачи контрольной работы: 1. Формирование основных приемов решения практических задач по темам дисциплины. 2. Формирование практических навыков использования математического материала в профессиональной деятельности. 3. Формирование умений строить математические модели, анализировать и содержательно интерпретировать полученные результаты, используя аппарат линейной алгебры и математического анализа.
2. Требования к результатам контрольной работы В результате выполнения контрольной работы студент должен: Знать: - методы линейной алгебры и аналитической геометрии; - методы дифференциального и интегрального исчислений; - функцию нескольких переменных; - ряды и их сходимость, разложение элементарных функций в ряд; - методы решения дифференциальных уравнений 1 и 2 порядка. Уметь: - исследовать функции, строить их графики; - вычислять производные и интегралы, в том числе для ФНП; - исследовать ряды на сходимость; - решать дифференциальные уравнения. Владеть: - навыками решения задач линейной алгебры и аналитической геометрии; - аппаратом дифференциального и интегрального исчислений функции одного и нескольких переменных; - навыками исследования числовых и функциональных рядов на сходимость; - навыками решения дифференциальных уравнений 1 и 2 порядка.
3. Объем самостоятельной работы студента Самостоятельная работа студента составляет 3,5 зачетные единицы по очной форме обучения, 6 зачетных единиц по заочной форме обучения.
4. Варианты контрольной работы
Вариант 1 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей
4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6. Найти производные функций: а) 7.Провести полное исследование функции 8. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а ) 13. Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости.
14. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
Вариант 2 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей
4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6. Найти производные функций:
7. Провести полное исследование функции 8.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости.
14. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
Вариант 3 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей 4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6. Найти производные функций:
7.Провести полное исследование функции и построить её график: 8.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям:
Вариант 4 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1)длины рёбер 1) угол между рёбрами 2) площадь грани 3) объём пирамиды; 4) уравнение плоскостей 4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6.Найти производные функций:
7.Провести полное исследование функции и построить её график:
8. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: Вариант 5 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей 4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6.Найти производные функций:
7. Провести полное исследование функции и построить её график:
8.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г). а) 9.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: Вариант 6 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей
4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6.Найти производные функций:
7.Провести полное исследование функции и построить её график:
8. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: Вариант 7 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей
4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6.Найти производные функций: а) 7.Провести полное исследование функции 8.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12.Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: Вариант 8 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей
4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6.Найти производные функций:
7.Провести полное исследование функции и построить её график:
8.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: Вариант 9 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей
4. Вычислить пределы функций:
5.Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6.Найти производные функций:
7.Провести полное исследование функции и построить её график:
8.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
Вариант 10 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: 1) методом Крамера; 2) методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
3. По координатам вершин пирамиды 1)длины рёбер 2)угол между рёбрами 3)площадь грани 4)объём пирамиды; 5)уравнение плоскостей
4. Вычислить пределы функций:
5. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
6.Найти производные функций:
7.Провести полное исследование функции 8.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Вычислить определённый интеграл (г).
9.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
10. Найти частные производные первого и второго порядка функций: а) 11. Исследовать на экстремум функцию 12. Исследовать на сходимость числовые ряды: а) 13. Найти радиус, интервал и область сходимости ряда: 14. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
Демонстрационный вариант контрольной работы 1. Вычислить матрицу 2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
3. По координатам вершин пирамиды 1) длины рёбер 2) угол между рёбрами 3) площадь грани 4) объём пирамиды; 5) уравнение плоскостей
4. Вычислить пределы функций:
5.Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.
|

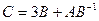 , где
, где 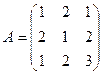 и
и  .
.
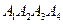 найти:
найти: и
и 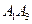 ;
; ;
; .
.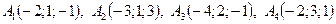 .
.

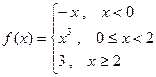
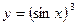 , б)
, б) 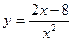 , в)
, в)  .
. и построить её график.
и построить её график.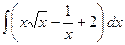 , б)
, б)  , в)
, в)  . г)
. г) 
 .
. б)
б) 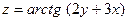
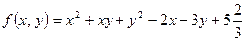 .
. ;б)
;б)  .
.
 ;
;  .
. , где
, где 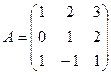 и
и  .
.
 .
.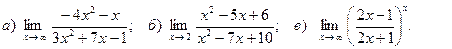

 , б)
, б)  , в)
, в) 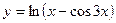 .
.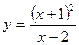 и построить её график.
и построить её график. , б)
, б) 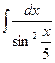 , в)
, в) 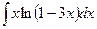 . г)
. г) 
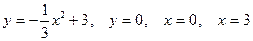 .
. б)
б) 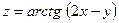
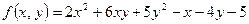 .
. ; б)
; б)  .
.
 ;
; 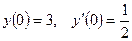 .
. , где
, где 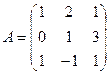 и
и  .
.
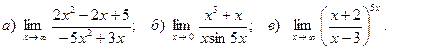
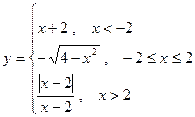
 , б)
, б)  , в)
, в) 
 .
. , б)
, б)  , в)
, в)  , г)
, г) 
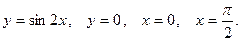
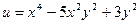 б)
б) 
 .
.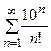 ; б)
; б) 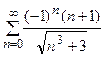 .
.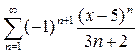 .
. ;
; 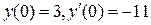 .
.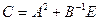 , где
, где 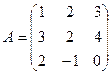 и
и 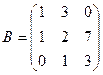 .
.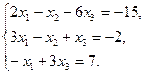


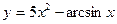 , б)
, б)  , в)
, в) 
 .
. , б)
, б)  , в)
, в)  .
.
 б)
б) 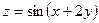
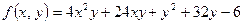 .
. ; б)
; б)  .
.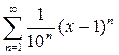 .
. ;
; 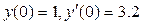 .
.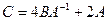 , где
, где 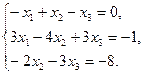


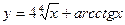 , б)
, б) 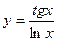 , в)
, в) 
 .
. , б)
, б)  , в)
, в) 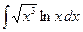 , г)
, г) 
 .
. б)
б) 
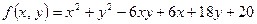 .
. ; б)
; б) 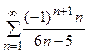 .
. .
.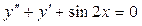 ;
;  .
. , где
, где  и
и  .
.
 .
.
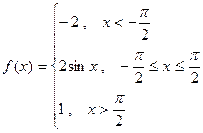
 , б)
, б) 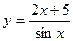 , в)
, в) 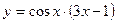
 .
.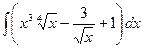 , б)
, б)  , в)
, в)  , г)
, г) 

 б)
б) 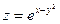
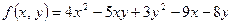 .
. ; б)
; б)  .
.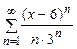 .
.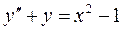 ;
; 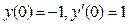 .
.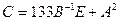 , где
, где  .
.
 .
.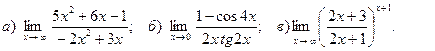
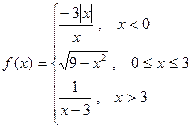
 , б)
, б) 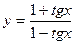 , в)
, в) 
 и построить её график.
и построить её график.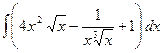 , б)
, б)  , в)
, в)  , г)
, г) 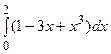

 б)
б) 
 .
. ; б)
; б) 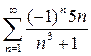 .
.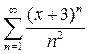 .
.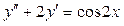 ;
; 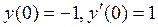 .
. , где
, где  и
и 
 .
.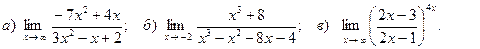
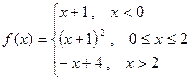
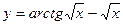 , б)
, б)  , в)
, в) 
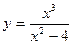 .
.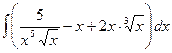 , б)
, б) 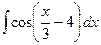 , в)
, в) 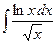 , г)
, г) 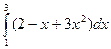
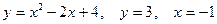 .
. б)
б) 
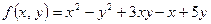 .
. ; б)
; б) 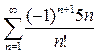 .
. .
. ;
; 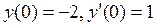 .
. , где
, где 
 .
.

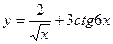 , б)
, б) 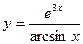 , в)
, в) 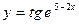
 .
.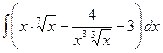 , б)
, б) 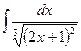 , в)
, в)  , г)
, г) 
 .
. б)
б) 
 .
. ; б)
; б) 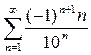 .
.
 ;
;  ,
, 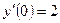 .
. , где
, где  и
и 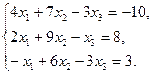
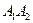 и
и  .
.
 , б)
, б)  , в)
, в) 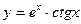
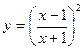 и построить её график.
и построить её график.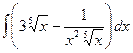 , б)
, б)  , в)
, в) 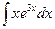 , г)
, г) 
 .
. б)
б) 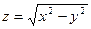
 .
. ; б)
; б) 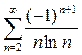 .
. .
. ;
; 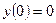 ,
,  , где
, где 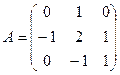 и
и 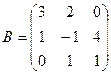 .
.
 .
.



